题目内容
【题目】如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D、E为BC边上的两点,且∠DAE=45°,连接EF、BF,则下列结论: ①△AED≌△AEF
②△AED为等腰三角形
③BE+DC>DE
④BE2+DC2=DE2 ,
其中正确的有( )个.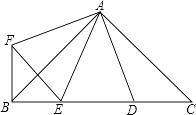
A.4
B.3
C.2
D.1
【答案】B
【解析】解:∵∠DAF=90°,∠DAE=45°, ∴∠FAE=45°=∠DAE,
在△AED与△AEF中,AE=AE,∠EAF=∠EAD,AD=AF,
∴△AED≌△AEF(SAS),①正确;
没有条件能证出△AED为等腰三角形,②错误;
∵∠BAC=∠DAF=90°,
∴∠BAF=∠DAC;
在△ABF与△ACD中,AB=AC,∠FAB=∠DAC,AF=AD,
∴△ABF≌△ACD(SAS),
∴BF=CD;
∵△AED≌△AEF,
∴DE=EF;
∵BE+BF>EF,而BF=CD,
∴BE+DC>DE,③正确;
∵∠EBF=90°,
∴BE2+BF2=EF2 ,
即BE2+DC2=DE2 , ④正确;
综上所述:①③④3个均正确,
故选B.
由SAS△AED≌△AEF,证明证明△ABF≌△ACD,得出BF=CD;由△AED≌△AEF,得到DE=EF;证明∠EBF=90°,即可解决问题.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目