��Ŀ����
����Ŀ������֪������ֱ���ҵ�ֱ��ƽ�������ң�����ƽ�����������Ե���������ƽ�ֻ���ֱ����ֱƽ�����������Ե��ң������������һ���۽�����⣺
��ͼ����P����MN���ϱ�����Ϊֱ���ġ�O�ϣ�MN=8��PQ��MN����O�ڵ�Q������ΪH��PQ��MN����PC��PD�ֱ�MN�ڵ�E��F����PE=PF��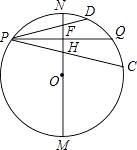
��1���Ƚ� ![]() ��
�� ![]() �Ĵ�С��
�Ĵ�С��
��2����OH=2 ![]() ����֤��OP��CD��
����֤��OP��CD��
��3����ֱ��MN��CD�ཻ���ɵ����Ϊ������ȷ��cos��= ![]() ʱ����P��λ�ã�
ʱ����P��λ�ã�
���𰸡�
��1���⣺��PE=PF��PH��EF��
��PHƽ�֡�FPE��
���DPQ=��CPQ��
�� ![]() =
= ![]() ��
��
��2��֤��������CD��OP��OQ��OQ��CD��B����ͼ��
��OH=2 ![]() ��OP=4��
��OP=4��
��PH= ![]() =2
=2 ![]() ��
��
���OPHΪ����ֱ�������Σ�
���OPQ=45�㣬
��OP=OQ��
���OPQΪ����ֱ�������Σ�
���POQ=90�㣬
��OP��OQ��
�� ![]() =
= ![]() ��
��
��OQ��CD��
��OP��CD
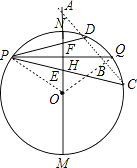
��3���⣺ֱ��CD��MN��A����ͼ��
��cos��= ![]() ��
��
��Ϧ�=30�㣬��ֱ��MN��CD�ཻ���ɵ����Ϊ30�㣬
��OB��CD��
���AOB=60�㣬
��OH��PQ��
���POH=60�㣬
��Rt��POH����sin��POH= ![]() ��
��
��PH=4sin60��=2 ![]() ��
��
����P��MN�ľ���Ϊ2 ![]() ��
��

����������1�����ݵ��������ε����ʣ���PE=PF��PH��EF���ж�PHƽ�֡�FPE��Ȼ�����Բ�нǶ����õ� ![]() =
= ![]() ����2������CD��OP��OQ��OQ��CD��B����ͼ���ȼ����PH=2
����2������CD��OP��OQ��OQ��CD��B����ͼ���ȼ����PH=2 ![]() ������жϡ�OPHΪ����ֱ�������εõ���OPQ=45�㣬���жϡ�OPQΪ����ֱ�������εõ���POQ=90�㣬Ȼ����ݴ�����������
������жϡ�OPHΪ����ֱ�������εõ���OPQ=45�㣬���жϡ�OPQΪ����ֱ�������εõ���POQ=90�㣬Ȼ����ݴ����������� ![]() =
= ![]() �õ�OQ��CD�������ƽ���ߵ��ж�������OP��CD����3��ֱ��CD��MN��A����ͼ��������ǵ����Ǻ���ֵ�áϦ�=30�㣬��ֱ��MN��CD�ཻ���ɵ����Ϊ30�㣬����OB��CD�õ���AOB=60�㣬���POH=60�㣬Ȼ����Rt��POH���������ҵĶ�������PH���ɣ����⿼����Բ���ۺ��⣺�������մ�����������������Բ�ܽǶ������ܹ����Ӧ�õ���ֱ�������ε����ʺ����Ǻ������м��μ��㣮
�õ�OQ��CD�������ƽ���ߵ��ж�������OP��CD����3��ֱ��CD��MN��A����ͼ��������ǵ����Ǻ���ֵ�áϦ�=30�㣬��ֱ��MN��CD�ཻ���ɵ����Ϊ30�㣬����OB��CD�õ���AOB=60�㣬���POH=60�㣬Ȼ����Rt��POH���������ҵĶ�������PH���ɣ����⿼����Բ���ۺ��⣺�������մ�����������������Բ�ܽǶ������ܹ����Ӧ�õ���ֱ�������ε����ʺ����Ǻ������м��μ��㣮

 ���ݼ���ϵ�д�
���ݼ���ϵ�д�


