题目内容
【题目】如图,在△ABC中,AC=BC=25,AB=30,D是AB上的一点(不与A、B重合),DE⊥BC,垂足是点E,设BD=x,四边形ACED的周长为y,则下列图象能大致反映y与x之间的函数关系的是( )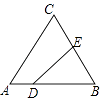
A.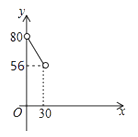
B.
C.
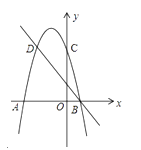
D.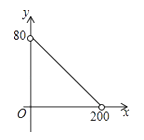
【答案】A
【解析】作CM⊥AB于M,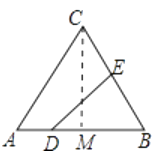
∵AC=BC=25,AB=30,
∴MA=MB=15,CM=![]() =20,
=20,
又∵DE⊥BC,
∴∠DEB=∠CMB,
又∵∠B=∠B,
∴△DBE∽△CBM,
∴![]() =
=![]() =
=![]() ,
,
又∵BD=x,BC=25,CM=20,MB=15,
∴![]() =
=![]() =
=![]() ,
,
∴DE=![]() x,BE=
x,BE=![]() x,
x,
∴AD=AB-BD=30-x,CE=CB-BE=25-![]() x,
x,
∴CACED=AD+DE+EC+CA=30-x+![]() x+25-
x+25-![]() x+25=80-
x+25=80-![]() x,
x,
即y=80-![]() x.
x.
又∵0![]() x
x![]() 30,
30,
∴图像为A.
故答案为:A.
作CM⊥AB于M,由等腰三角形的性质得出MA=MB=15,由勾股定理得出CM=20,根据相似三角形的判定得出△DBE∽△CBM;由相似三角形的性质得出DE=![]() x,BE=
x,BE=![]() x,AD=30-x,CE=25-
x,AD=30-x,CE=25-![]() x,根据四边形的周长得出y=80-
x,根据四边形的周长得出y=80-![]() x.从而得出其函数图像.
x.从而得出其函数图像.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目