题目内容
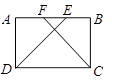
如图，在等腰梯形ABCD中，AD∥BC，AB＝AD=DC，AC = BC。则∠B的度数是：
A. 45° B. 60° C. 72° D. 80°
A. 45° B. 60° C. 72° D. 80°
C
∵AD=DC，∴∠DAC=∠DCA，∵AD∥BC，∴∠DAC=∠ACB=∠DCA，
∵等腰梯形ABCD，AD∥BC，AB=DC，∴∠B=∠DCB=2∠ACB，∵AC=BC，∴∠B=∠BAC，
设∠ACB=a°，则∠B=∠BAC=2a°，∵∠B+∠ACB+∠BAC=180°，∴2a+2a+a=180，∴a=36°，
即∠B=2a°=72°．故选C．
∵等腰梯形ABCD，AD∥BC，AB=DC，∴∠B=∠DCB=2∠ACB，∵AC=BC，∴∠B=∠BAC，
设∠ACB=a°，则∠B=∠BAC=2a°，∵∠B+∠ACB+∠BAC=180°，∴2a+2a+a=180，∴a=36°，
即∠B=2a°=72°．故选C．
练习册系列答案
相关题目
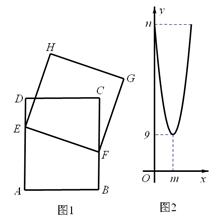
上的两点，且
.
；
.
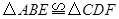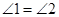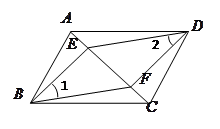
ABCD中，E，F分别是BC、AD上的点，且BE=DF．求证：AE=CF．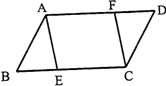
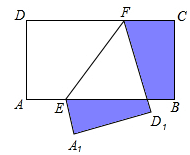
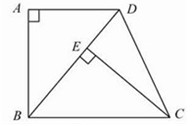
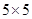方格中,每个小正方形的边长都是
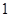,按下列要求画格点梯形(顶点都在格点上的梯形)并直接写出所画梯形的周长.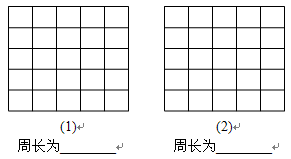
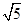的梯形;