题目内容
【题目】已知线段![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 上一点,连接
上一点,连接![]() 交于
交于![]() 点.
点.
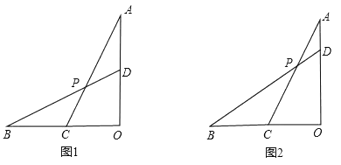
(1)如图1,当![]() 且
且![]() 为
为![]() 中点时,求
中点时,求![]() 的值.
的值.
(2)如图2,当![]() ,
,![]() =
=![]() 时,求tan∠
时,求tan∠![]() 的值.
的值.
【答案】(1)![]() ;(2)tan∠BPC=
;(2)tan∠BPC=![]() .
.
【解析】
(1)连结AB、CD,首先证明点P为△OAB的重心,得到![]() ,然后利用勾股定理求出AP即可;
,然后利用勾股定理求出AP即可;
(2)延长AC至点H,使CH=CA,连接BH,易证△BCH≌△OCA,得到BH=OA,∠CBH=∠O,然后设AD=t,OD=3t,则BH=OA=OB=4t,根据△HBP∽△ADP列比例式求出BP=4t,得到BH=BP,然后根据tan∠BPC=tan∠H求解即可.
解:(1)连结AB、CD,
∵C、D分别为OB、OA的中点,
∴AC、BD为△OAB边OB、OA的中线,
∴点P为△OAB的重心,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴在Rt△AOC中,![]() ,
,
∴![]() ;
;
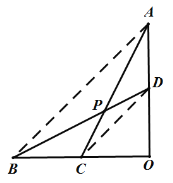
(2)延长AC至点H,使CH=CA,连接BH,
∵C是OB的中点,
易得△BCH≌△OCA(SAS),
∴BH=OA,∠CBH=∠O,
由![]() ,设AD=t,OD=3t,则BH=OA=OB=4t,
,设AD=t,OD=3t,则BH=OA=OB=4t,
在Rt△BOD中,BD=![]() ,
,
∵∠CBH=∠O,
∴OA//BH,
∴△HBP∽△ADP,
∴![]() ,
,
∴BP=4PD=![]() BD=4t,
BD=4t,
∴BH=BP,
∴∠BPC=∠H,
∴tan∠BPC=tan∠H=![]() =
=![]() =
=![]() .
.

【题目】在水果销售旺季,某水果店购进一优质水果,进价为20元/千克,售价不低于20元/千克,且不超过32元/千克,根据销售情况,发现该水果一天的销售量y(千克)与该天的售价x(元/千克)满足如下表所示的一次函数关系.
销售量y(千克) | … | 34.8 | 32 | 29.6 | 28 | … |
售价x(元/千克) | … | 22.6 | 24 | 25.2 | 26 | … |
(1)某天这种水果的售价为23.5元/千克,则当天该水果的销售量 千克.
(2)如果某天销售这种水果获利150元,那么该天水果的售价为多少元?
(3)当售价定为多少元时,当天销售这种水果获利最大?最大利润是多少?