题目内容
平面直角坐标系与线段和的最值问题:
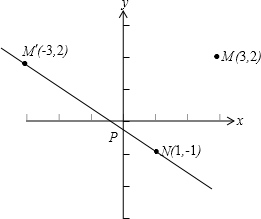
(1)已知点M(3,2),N(1,-1),点P在y轴上,求使得△PMN的周长最小的点P的坐标;
(2)等腰梯形ABCD放置在如图所示的直角平面坐标系中,已知CD∥AB,CD=3,AB=5,BC=
,直线AC交y轴于E,动点P在线段EC上运动,求点P到y轴的距离与点P到点N(2,6)的距离之和的最小值,并求出此时的点P的坐标.

(1)已知点M(3,2),N(1,-1),点P在y轴上,求使得△PMN的周长最小的点P的坐标;
(2)等腰梯形ABCD放置在如图所示的直角平面坐标系中,已知CD∥AB,CD=3,AB=5,BC=
| 17 |

(1)如图所示,作出M关于y轴的对称点M′,连接NM′,与y轴相交于点P,则P点即为所求,
设过NM′两点的直线解析式为y=kx+b(k≠0),
则
,解得k=-
,b=-
,
故此一次函数的解析式为y=-
x-
,
因为b=-
,所以P点坐标为(0,-
);
(2)作出点N关于直线AE的对称点N′,CH⊥AB,过N′向y轴作垂线,交y轴于点Q,交直线AF于点P,则QN′即为点P到y轴的距离与点P到点N的距离之和的最小值,
∵等腰梯形ABCD中,CD∥AB,CD=3,AB=5,BC=
,
∴OA=HB=1,
∴A(-1,0),B(4,0)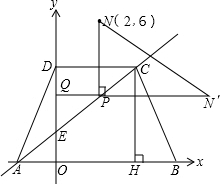
∴CH=
=
=4,
∴D(0,4)、C(3,4),
设直线AE的解析式为y=kx+b(k≠0),
则
,解得k=1,b=1,
∴直线AE的解析式为y=x+1,
∴N′点的坐标为(5,3),
∴QN′=5;
设P点坐标为(a,3),代入直线y=x+1得,3=a+1,解得a=2,
∴P点坐标为(2,3).
设过NM′两点的直线解析式为y=kx+b(k≠0),
则
|
| 3 |
| 4 |
| 1 |
| 4 |
故此一次函数的解析式为y=-
| 3 |
| 4 |
| 1 |
| 4 |
因为b=-
| 1 |
| 4 |
| 1 |
| 4 |
(2)作出点N关于直线AE的对称点N′,CH⊥AB,过N′向y轴作垂线,交y轴于点Q,交直线AF于点P,则QN′即为点P到y轴的距离与点P到点N的距离之和的最小值,
∵等腰梯形ABCD中,CD∥AB,CD=3,AB=5,BC=
| 17 |
∴OA=HB=1,
∴A(-1,0),B(4,0)

∴CH=
| BC2-HB2 |
(
|
∴D(0,4)、C(3,4),
设直线AE的解析式为y=kx+b(k≠0),
则
|
∴直线AE的解析式为y=x+1,
∴N′点的坐标为(5,3),
∴QN′=5;
设P点坐标为(a,3),代入直线y=x+1得,3=a+1,解得a=2,
∴P点坐标为(2,3).


练习册系列答案
相关题目






