Question

【题目】乐乐发现等腰三角形一腰上的高与另一腰的夹角为40°，则这个等腰三角形底角的度数为（ ）

A.50°B.65°C.65°或25°D.50°或40°

Answer 1

【答案】C

【解析】

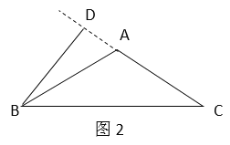
在等腰△ABC中，AB= AC，BD为腰AC上的高，∠ABD=40°，讨论：当BD在ABC内部时，如图1，先计算出∠BAD=50°，再根据等腰三角形的性质和三角形内角和可计算出∠ACB；当BD在△ABC外部时，如图2，先计算出∠BAD=50°，再根据等腰三角形的性质和三角形外角性质可计算出∠ACB.

在等腰△ABC中，AB= AC，BD为腰AC上的高，∠ABD=40°，

当BD在△ABC内部时，如图1，
∵BD是高，
∴∠ADB=90°，
∴∠BAD=90°-40°=50°，
∵AB=AC，
∴∠ABC=∠ACB=(180°-50°)=65°；
当BD在△ABC外部时，如图2，
∵BD是高，
∴∠ADB=90°，
∴∠BAD=90°-40°=50°，

∵AB=AC，
∴∠ABC=∠ACB，
∵∠BAD=∠ABC+∠ACB,
∴∠ACB=∠BAD=25°，

综上，这个等腰三角形底角的度数为65°或25°.

故选：C.