Question

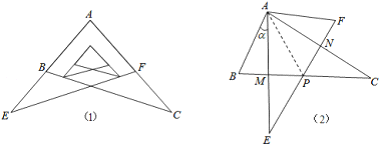
【题目】如图，在△ABC中，∠C=90°，点P是斜边AB的中点，点M从点C向点A匀速运动，点N从点B向点C匀速运动，已知两点同时出发，同时到达终点，连接PM、PN、MN，在整个运动过程中，△PMN的面积S与运动时间t的函数关系图象大致是（ ）

Answer 1

【答案】A

【解析】

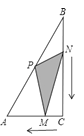
试题分析：如图，连接CP，由点P是斜边AB的中点，可得S△ACP=S△BCP=S△ABC，出发时，点M和点C重合，点N和点B重合，S△PMN=S△BCP=S△ABC；又因两点同时出发，同时到达终点，可得点N到达BC的中点时，点M也到达AC的中点，这时可得S△PMN=S△ABC；结束时，点M和点A重合，点N和点C重合，S△PMN=S△ACP=S△ABC，由此可得△MPQ的面积大小变化情况是：先减小后增大，而且是以抛物线的方式变化，故答案选A．

试题解析：解：如图，连接CP，

∵点P是斜边AB的中点，

∴，

出发时，,

∵两点同时出发，同时到达终点，

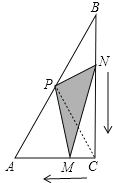
∴点N到达BC的中点时，点M也到达AC的中点，

∴，

结束时，，

在整个运动过程中，设，

∴

∴△MPQ的面积大小变化情况是：先减小后增大，而且是以抛物线的方式变化，故选A.