题目内容
【题目】四边形ABCD中,E是AB边上的一个动点(不与点A、B重合),连接DE,过点E作EP⊥DE.
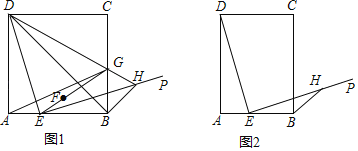
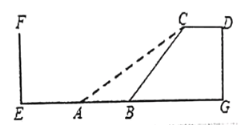
(1)如图1,当四边形ABCD是正方形时,点A关于直线DE的对称点为点F,连接EF并延长交BC于点G;射线DG交EP于点H,连接BH.
①求证:GF=GC
②请求出![]() 的值;
的值;
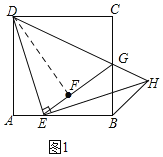
(2)如图2,四边形ABCD是矩形,且AD=kAB,点H是射线EP上的一点,连接BH,当DE=kEH时,请直接写出![]() 的值.
的值.
【答案】(1)①详见解析;②![]() ;(2)
;(2)![]() .
.
【解析】
(1)①如图1,连接DF,根据对称得:△ADE≌△FDE,再由HL证明Rt△DFG≌Rt△DCG,即可得出结论;
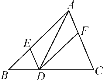
②如图2,作辅助线,构建AM=AE,先证明∠EDG=45°,得DE=EH,证明△DME≌△EBH,则EM=BH,根据等腰直角的性质得:EM=![]() AE,即可得出结论;
AE,即可得出结论;
(2)先构建AM=kAE,进而得出![]() =k,即可得出
=k,即可得出![]() ,进而判断出△MDE∽△BEH,得出
,进而判断出△MDE∽△BEH,得出![]() =k,再判断出ME=
=k,再判断出ME=![]() AE,即可得出结论.
AE,即可得出结论.
证明:(1)①如图1,连接DF,
∵四边形ABCD是正方形,
∴DA=DC,∠A=∠C=90°,
∵点A关于直线DE的对称点为F,
∴△ADE≌△FDE,
∴DA=DF=DC,∠DFE=∠A=90°,
∴∠DFG=90°,
在Rt△DFG和Rt△DCG中,
∵![]() ,
,
∴Rt△DFG≌Rt△DCG(HL),
∴GF=GC;
②如图2,在线段AD上截取AM,使AM=AE,
∵AD=AB,
∴DM=BE,
由①知:∠1=∠2,∠3=∠4,
∵∠ADC=90°,
∴∠1+∠2+∠3+∠4=90°,
∴2∠2+2∠3=90°,
∴∠2+∠3=45°,
即∠EDG=45°,
∵EH⊥DE,
∴∠DEH=90°,△DEH是等腰直角三角形,
∴∠AED+∠BEH=∠AED+∠1=90°,DE=EH,
∴∠1=∠BEH,
在△DME和△EBH中,
∵ ,
,
∴△DME≌△EBH(SAS),
∴EM=BH,
Rt△AEM中,∠A=90°,AM=AE,
∴EM=![]() AE,
AE,
∴BH=![]() AE,
AE,
∴![]() =
=![]() ;
;
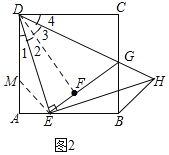
(2)如图3,
在AD上截取AM,使AM=kAE,
∵AD=kAB,
∴DM=AD﹣AM=kAB﹣kAE=k(AB﹣AE)=kBE,
∴![]() =k
=k
∵DE=kEH,
∴![]() =k,
=k,
∴![]() ,
,
同①的方法得,∠MDE=∠BEH,
∴△MDE∽△BEH,
∴![]() =k,
=k,
在Rt△EAM中,ME=![]() ,
,
∴![]() ,
,
∴![]() =
=![]() .
.

【题目】甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:
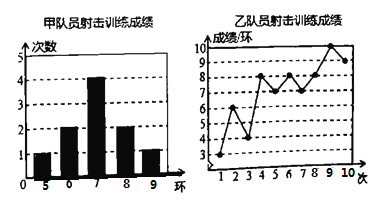
根据以上信息,整理分析数据如下:
平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
甲 |
|
|
|
|
乙 |
|
|
|
|
(1)写出表格中![]() 的值:
的值:
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?