题目内容
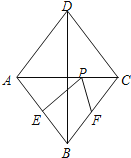
【题目】如图,在菱形ABCD中,对角线AC=6,BD=8,点E、F分别是边AB、BC的中点,点P在AC上运动,在运动过程中,存在PE+PF的最小值,则这个最小值是________________
【答案】5
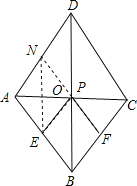
【解析】试题分析:AC交BD于O,作E关于AC的对称点N,连接NF,交AC于P,则此时EP+FP的值最小,
∴PN=PE, ∵四边形ABCD是菱形, ∴∠DAB=∠BCD,AD=AB=BC=CD,OA=OC,OB=OD,AD∥BC,
∵E为AB的中点, ∴N在AD上,且N为AD的中点, ∵AD∥CB, ∴∠ANP=∠CFP,∠NAP=∠FCP,
∵AD=BC,N为AD中点,F为BC中点, ∴AN=CF, ∴△ANP≌△CFP(ASA), ∴AP=CP,
即P为AC中点, ∵O为AC中点, ∴P、O重合, 即NF过O点, ∵AN∥BF,AN=BF,
∴四边形ANFB是平行四边形, ∴NF=AB, ∵菱形ABCD,
∴AC⊥BD,OA=![]() AC=3,BO=
AC=3,BO=![]() BD=4,由勾股定理得:AB=5,
BD=4,由勾股定理得:AB=5,

练习册系列答案
相关题目
【题目】(6分)在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,表是活动进行中的一组统计数据:
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到白球的次数m | 68 | 109 | 136 | 345 | 368 | 701 |
摸到乒乓球的频率 | 0.68 | 0.73 | 0.68 | 0.69 | 0.70 | 0.70 |
(1)请估计:当n很大时,摸到白球的频率将会接近________;
(2)假如你去摸一次,你摸到白球的概率是_______,摸到黑球的概率是_______;
(3)试估算口袋中黑、白两种颜色的球各有多少只?