Question

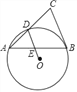
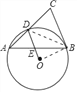
【题目】如图，△ABC中，∠A=45°，D是AC边上一点，⊙O经过D、A、B三点，OD∥BC．

（1）求证：BC与⊙O相切；

（2）若OD=15，AE=7，求BE的长．

Answer 1

【答案】(1)见解析;(2)18.

【解析】分析：（1）连接OB，求出∠DOB度数，根据平行线性质求出∠CBO=90°，根据切线判定得出即可；
（2）延长BO交⊙O于点F，连接AF，求出∠ABF，解直角三角形求出BE．

详解：（1）证明：连接OB．

∵∠A=45°，

∴∠DOB=90°．

∵OD∥BC，

∴∠DOB+∠CBO=180°．

∴∠CBO=90°．

∴直线BC是⊙O的切线．

（2）解：连接BD．则△ODB是等腰直角三角形，

∴∠ODB=45°，BD=OD=15，

∵∠ODB=∠A，∠DBE=∠DBA，

∴△DBE∽△ABD，

∴BD2=BEBA，

∴（15）2=（7+BE）BE，

∴BE=18或﹣25（舍弃），

∴BE=18．