题目内容
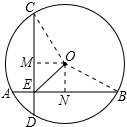
如图,⊙O的两条弦AB、CD互相垂直,垂足为点E,当⊙O的半径为2,AB与CD两弦长的平方和等于28,则OE等于______.


如图,过O分别作AB、CD的垂线,垂足分别为N,M,然后连接OC,OB,
∵AB⊥CD,
∴四边形OMEN是矩形,
∴ON=ME,OM=EN,
在Rt△COM中,OC2-CM2=OM2,
在Rt△BON中,OB2-BN2=ON2,而BN=
AB,CM=
CD,
又∵OE2=ON2+MO2,
∴OE2=ON2+MO2=OC2-CM2+OB2-BN2=2OB2-
(AB2+CD2),
又∵⊙O的半径为2,AB与CD两弦长的平方和等于28,
∴OE2=8-7=1,
∴OE=1.
故答案为:1.
∵AB⊥CD,
∴四边形OMEN是矩形,
∴ON=ME,OM=EN,
在Rt△COM中,OC2-CM2=OM2,
在Rt△BON中,OB2-BN2=ON2,而BN=
| 1 |
| 2 |
| 1 |
| 2 |
又∵OE2=ON2+MO2,
∴OE2=ON2+MO2=OC2-CM2+OB2-BN2=2OB2-
| 1 |
| 4 |
又∵⊙O的半径为2,AB与CD两弦长的平方和等于28,
∴OE2=8-7=1,
∴OE=1.
故答案为:1.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目