题目内容
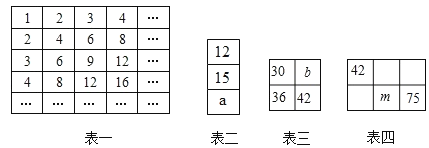
【题目】如图是由从1开始的连续自然数组成,则第8行第8 个数是________,第n 行第一个数可表示为___.

【答案】15 n2-2n+2
【解析】
通过观察可得第n行最后一数为n2,即可得出第8行的最后一个数是82,第8行的数字个数正好是第8行的最后一个数减去第7行的最后一个数,从而得出答案;通过前面的规律,即可得出第n 行第一个数的答案.
每行数的个数为1,3,5,…的奇数列,由题意最后一个数是该行数的平方,得:
表中第8行的最后一个数是82=64,
第8行共有82-72=64-49=15个数;
所以第n-1行最后一个数为:(n-1)2,
则第n行的第一个数是:(n-1)2+1=n2-2n+2;
故答案为:15,n2-2n+2;

练习册系列答案
相关题目