Question

【题目】已知ABCD的周长为36cm，过点A作AE⊥BC，AF⊥CD，垂足分别为E、F.若AE＝2cm，AF＝4cm.求ABCD的各边长．

Answer 1

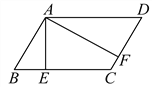
【答案】AB＝CD＝6cm，AD＝BC＝12cm.

【解析】【试题分析】根据ABCD的周长为36cm，得BC＋CD＝18；根据等面积法，得SABCD＝BC·AE＝CD·AF，解得：BC＝2CD，两式联立方程组，，解得，根据平行四边形的对边相等，得AB＝CD＝6cm，AD＝BC＝12cm.

【试题解析】

∵ABCD中，AB＝CD，BC＝AD，又∵ABCD的周长为36cm.即AB＋BC＋CD＋AD＝36，即BC＋CD＝18，又∵SABCD＝BC·AE＝CD·AF，∴2BC＝4CD，即BC＝2CD，解方程组，得，∴AB＝CD＝6cm，AD＝BC＝12cm.