题目内容
如果一条抛物线的形状与y=- x2+2的形状相同,且顶点坐标是(4,-2),那么它的函数解析式为
x2+2的形状相同,且顶点坐标是(4,-2),那么它的函数解析式为
- A.
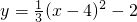
- B.
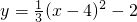 或
或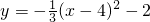
- C.
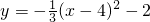
- D.
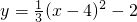 或
或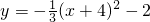
B
分析:本题从题干中的条件入手,由给出的抛物线的形状相同可判断出|a|相等,又由顶点坐标可判断出正确选项.
解答:设所求抛物线的解析式为y=ax2+bx+c,由形状与y=- x2+2的形状相同,则|a|=
x2+2的形状相同,则|a|= ,
,
又抛物线过顶点坐标(4,-2),则由此可判断出B选项的函数解析式符合题意.
故选B.
点评:本题考查了待定系数法求二次函数解析式的方法,在这里用排除法更为简单.
分析:本题从题干中的条件入手,由给出的抛物线的形状相同可判断出|a|相等,又由顶点坐标可判断出正确选项.
解答:设所求抛物线的解析式为y=ax2+bx+c,由形状与y=-
 x2+2的形状相同,则|a|=
x2+2的形状相同,则|a|= ,
,又抛物线过顶点坐标(4,-2),则由此可判断出B选项的函数解析式符合题意.
故选B.
点评:本题考查了待定系数法求二次函数解析式的方法,在这里用排除法更为简单.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如果一条抛物线的形状与y=-
x2+2的形状相同,且顶点坐标是(4,-2),那么它的函数解析式为( )
| 1 |
| 3 |
A、y=
| ||||
B、y=
| ||||
C、y=-
| ||||
D、y=
|
 的形状相同,且顶点坐标是(4,2),则它的解析式为 .
的形状相同,且顶点坐标是(4,2),则它的解析式为 .