题目内容
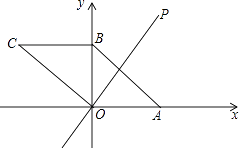
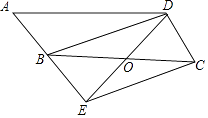
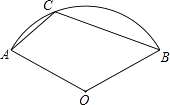
【题目】如图,已知△ABC中,∠C=90°,点M从点C出发沿CB方向以1cm/s的速度匀速运动,到达点B停止运动,在点M的运动过程中,过点M作直线MN交AC于点N,且保持∠NMC=45°,再过点N作AC的垂线交AB于点F,连接MF,将△MNF关于直线NF对称后得到△ENF,已知AC=8cm,BC=4cm,设点M运动时间为t(s),△ENF与△ANF重叠部分的面积为y(cm2).
(1)在点M的运动过程中,能否使得四边形MNEF为正方形?如果能,求出相应的t值;如果不能,说明理由;
(2)求y关于t的函数解析式及相应t的取值范围;
(3)当y取最大值时,求sin∠NEF的值.
【答案】
(1)
解:能使得四边形MNEF为正方形;理由如下:
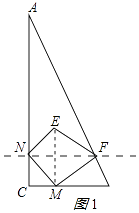
连接ME交NF于O,如图1所示:
∵∠C=90°,∠NMC=45°,NF⊥AC,
∴CN=CM=t,FN∥BC,
∴AN=8﹣t,△ANF∽△ACB,
∴ ![]() =
= ![]() =2,
=2,
∴NF= ![]() AN=
AN= ![]() (8﹣t),
(8﹣t),
由对称的性质得:∠ENF=∠MNF=∠NMC=45°,MN=NE,OE=OM=CN=t,
∵四边形MNEF是正方形,
∴OE=ON=FN,
∴t= ![]() ×
× ![]() (8﹣t),
(8﹣t),
解得:t= ![]() ;
;
即在点M的运动过程中,能使得四边形MNEF为正方形,t的值为 ![]() ;
;
(2)
解:分两种情况:
①当0<t≤2时,y= ![]() ×
× ![]() (8﹣t)×t=﹣
(8﹣t)×t=﹣ ![]() t2+2t,
t2+2t,
即y=﹣ ![]() t2+2t(0<t≤2);
t2+2t(0<t≤2);
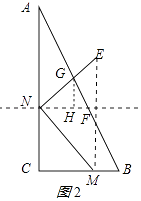
②当2<t≤4时,如图2所示:作GH⊥NF于H,
由(1)得:NF= ![]() (8﹣t),GH=NH,GH=2FH,
(8﹣t),GH=NH,GH=2FH,
∴GH= ![]() NF=
NF= ![]() (8﹣t),
(8﹣t),
∴y= ![]() NF′GH=
NF′GH= ![]() ×
× ![]() (8﹣t)×
(8﹣t)× ![]() (8﹣t)=
(8﹣t)= ![]() (8﹣t)2,
(8﹣t)2,
即y= ![]() (8﹣t)2(2<t≤4);
(8﹣t)2(2<t≤4);
(3)
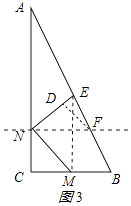
解:当点E在AB边上时,y取最大值,
连接EM,如图3所示:
则EF=BF,EM=2CN=2CM=2t,EM=2BM,
∵BM=4﹣t,
∴2t=2(4﹣t),
解得:t=2,
∴CN=CM=2,AN=6,
∴BM=4﹣2=2,NF= ![]() AN=3,
AN=3,
∴EM=2BM=4,
作FD⊥NE于D,则EB= ![]() =
= ![]() =2
=2 ![]() ,△DNF是等腰直角三角形,
,△DNF是等腰直角三角形,
∴EF= ![]() =
= ![]() ,DF=
,DF= ![]() HF=
HF= ![]() ,
,
在Rt△DEF中,sin∠NEF= ![]() =
= ![]() =
= ![]() .
.
【解析】(1)由已知得出CN=CM=t,FN∥BC,得出AN=8﹣t,由平行线证出△ANF∽△ACB,得出对应边成比例求出NF= ![]() AN=
AN= ![]() (8﹣t),由对称的性质得出∠ENF=∠MNF=∠NMC=45°,MN=NE,OE=OM=CN=t,由正方形的性质得出OE=ON=FN,得出方程,解方程即可;(2)分两种情况:①当0<t≤2时,由三角形面积得出y=﹣
(8﹣t),由对称的性质得出∠ENF=∠MNF=∠NMC=45°,MN=NE,OE=OM=CN=t,由正方形的性质得出OE=ON=FN,得出方程,解方程即可;(2)分两种情况:①当0<t≤2时,由三角形面积得出y=﹣ ![]() t2+2t;②当2<t≤4时,作GH⊥NF于H,由(1)得:NF=
t2+2t;②当2<t≤4时,作GH⊥NF于H,由(1)得:NF= ![]() (8﹣t),GH=NH,GH=2FH,得出GH=
(8﹣t),GH=NH,GH=2FH,得出GH= ![]() NF=
NF= ![]() (8﹣t),由三角形面积得出y=
(8﹣t),由三角形面积得出y= ![]() (8﹣t)2(2<t≤4);(3)当点E在AB边上时,y取最大值,连接EM,则EF=BF,EM=2CN=2CM=2t,EM=2BM,得出方程,解方程求出CN=CM=2,AN=6,得出BM=2,NF=
(8﹣t)2(2<t≤4);(3)当点E在AB边上时,y取最大值,连接EM,则EF=BF,EM=2CN=2CM=2t,EM=2BM,得出方程,解方程求出CN=CM=2,AN=6,得出BM=2,NF= ![]() AN=3,因此EM=2BM=4,作FD⊥NE于D,由勾股定理求出EB=
AN=3,因此EM=2BM=4,作FD⊥NE于D,由勾股定理求出EB= ![]() =2
=2 ![]() ,求出EF=
,求出EF= ![]() =
= ![]() ,由等腰直角三角形的性质和勾股定理得出DF=
,由等腰直角三角形的性质和勾股定理得出DF= ![]() HF=
HF= ![]() ,在Rt△DEF中,由三角函数定义即可求出sin∠NEF的值.
,在Rt△DEF中,由三角函数定义即可求出sin∠NEF的值.
【考点精析】掌握相似三角形的判定与性质是解答本题的根本,需要知道相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

【题目】红星中学课外兴趣活动小组对某水稻品种的稻穗谷粒数目进行调查,从试验田中随机抽取了30株,得到的数据如下(单位:颗):
182 | 195 | 201 | 179 | 208 | 204 | 186 | 192 | 210 | 204 |
175 | 193 | 200 | 203 | 188 | 197 | 212 | 207 | 185 | 206 |
188 | 186 | 198 | 202 | 221 | 199 | 219 | 208 | 187 | 224 |
(1)对抽取的30株水稻稻穗谷粒数进行统计分析,请补全下表中空格,并完善直方图:
谷粒颗数 | 175≤x<185 | 185≤x<195 | 195≤x<205 | 205≤x<215 | 215≤x<225 |
频数 | 8 | 10 | 3 | ||
对应扇形图中区域 | D | E | C |

如图所示的扇形统计图中,扇形A对应的圆心角为 度,扇形B对应的圆心角为 度;
(2)该试验田中大约有3000株水稻,据此估计,其中稻穗谷粒数大于或等于205颗的水稻有多少株?