题目内容
(2012•长沙)如图半径分别为m,n(0<m<n)的两圆⊙O1和⊙O2相交于P,Q两点,且点P(4,1),两圆同时与两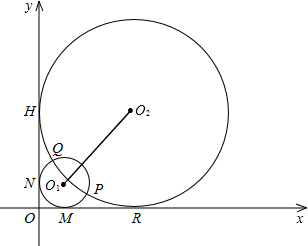 坐标轴相切,⊙O1与x轴,y轴分别切于点M,点N,⊙O2与x轴,y轴分别切于点R,点H.
坐标轴相切,⊙O1与x轴,y轴分别切于点M,点N,⊙O2与x轴,y轴分别切于点R,点H.
(1)求两圆的圆心O1,O2所在直线的解析式;
(2)求两圆的圆心O1,O2之间的距离d;
(3)令四边形PO1QO2的面积为S1,四边形RMO1O2的面积为S2.
试探究:是否存在一条经过P,Q两点、开口向下,且在x轴上截得的线段长为
的抛物线?若存在,请求出此抛物线的解析式;若不存在,请说明理由.
 坐标轴相切,⊙O1与x轴,y轴分别切于点M,点N,⊙O2与x轴,y轴分别切于点R,点H.
坐标轴相切,⊙O1与x轴,y轴分别切于点M,点N,⊙O2与x轴,y轴分别切于点R,点H.(1)求两圆的圆心O1,O2所在直线的解析式;
(2)求两圆的圆心O1,O2之间的距离d;
(3)令四边形PO1QO2的面积为S1,四边形RMO1O2的面积为S2.
试探究:是否存在一条经过P,Q两点、开口向下,且在x轴上截得的线段长为
| |s1-s2| | ||
|
分析:(1)根据直线过点O1(m,m),O2(n,n),利用待定系数法求出其解析式;
(2)本问有一定难度.可分以下步骤解决:
第1步:首先根据P、Q关于连心线对称,求出Q点的坐标;
第2步:求出m、n.利用两点间的距离公式,求出O1Q,而O1Q=m,从而得到关于m的一元二次方程,求解即可得到m的大小;同理求得n;
第3步:利用两点间距离公式求d.
(3)本问有一定难度.可分以下步骤解决:
第1步:假设存在这样的抛物线,其解析式为y=ax2+bx+c,因为开口向下,所以a<0;
第2步:求出S1、S2,再代入计算得:
=1,即抛物线在x轴上截得的线段长为1;
第3步:根据抛物线过点P(4,1),Q(1,4),用待定系数法求得其解析式为:y=ax2-(5a+1)x+5+4a;
第4步:由抛物线在x轴上截得的线段长为1,即|x1-x2|=1,得到关于a的一元二次方程,此方程的两个根均大于0,这与抛物线开口向下(a<0)相矛盾,所以得出结论:这样的抛物线不存在.
(2)本问有一定难度.可分以下步骤解决:
第1步:首先根据P、Q关于连心线对称,求出Q点的坐标;
第2步:求出m、n.利用两点间的距离公式,求出O1Q,而O1Q=m,从而得到关于m的一元二次方程,求解即可得到m的大小;同理求得n;
第3步:利用两点间距离公式求d.
(3)本问有一定难度.可分以下步骤解决:
第1步:假设存在这样的抛物线,其解析式为y=ax2+bx+c,因为开口向下,所以a<0;
第2步:求出S1、S2,再代入计算得:
| |s1-s2| | ||
|
第3步:根据抛物线过点P(4,1),Q(1,4),用待定系数法求得其解析式为:y=ax2-(5a+1)x+5+4a;
第4步:由抛物线在x轴上截得的线段长为1,即|x1-x2|=1,得到关于a的一元二次方程,此方程的两个根均大于0,这与抛物线开口向下(a<0)相矛盾,所以得出结论:这样的抛物线不存在.
解答:解:(1)由题意可知O1(m,m),O2(n,n),
设过点O1,O2的直线解析式为y=kx+b,则有:
(0<m<n),解得
,
∴所求直线的解析式为:y=x.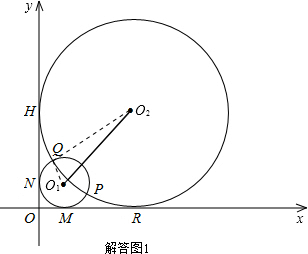
(2)由相交两圆的性质,可知P、Q点关于O1O2对称.
∵P(4,1),直线O1O2解析式为y=x,∴Q(1,4).
如解答图1,连接O1Q.
∵Q(1,4),O1(m,m),根据两点间距离公式得到:
O1Q=
=
又O1Q为小圆半径,即QO1=m,
∴
=m,化简得:m2-10m+17=0 ①
如解答图1,连接O2Q,同理可得:n2-10n+17=0 ②
由①,②式可知,m、n是一元二次方程x2-10x+17=0 ③的两个根,
解③得:x=5±2
,∵0<m<n,∴m=5-2
,n=5+2
.
∵O1(m,m),O2(n,n),
∴d=O1O2=
=8.
(3)假设存在这样的抛物线,其解析式为y=ax2+bx+c,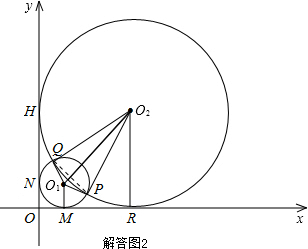 因为开口向下,所以a<0.
因为开口向下,所以a<0.
如解答图2,连接PQ.
由相交两圆性质可知,PQ⊥O1O2.
∵P(4,1),Q(1,4),
∴PQ=
=3
,又O1O2=8,
∴S1=
PQ•O1O2=
×3
×8=12
;
又S2=
(O2R+O1M)•MR=
(n+m)(n-m)=20
;
∴
=
=1,即抛物线在x轴上截得的线段长为1.
∵抛物线过点P(4,1),Q(1,4),
∴
,解得
,
∴抛物线解析式为:y=ax2-(5a+1)x+5+4a,
令y=0,则有:ax2-(5a+1)x+5+4a=0,
设两根为x1,x2,则有:x1+x2=
,x1x2=
,
∵在x轴上截得的线段长为1,即|x1-x2|=1,
∴(x1-x2)2=1,∴(x1+x2)2-4x1x2=1,
即(
)2-4(
)=1,化简得:8a2-10a+1=0,
解得a=
,可见a的两个根均大于0,这与抛物线开口向下(即a<0)矛盾,
∴不存在这样的抛物线.
设过点O1,O2的直线解析式为y=kx+b,则有:
|
|
∴所求直线的解析式为:y=x.

(2)由相交两圆的性质,可知P、Q点关于O1O2对称.
∵P(4,1),直线O1O2解析式为y=x,∴Q(1,4).
如解答图1,连接O1Q.
∵Q(1,4),O1(m,m),根据两点间距离公式得到:
O1Q=
| (m-1)2+(m-4)2 |
| 2m2-10m+17 |
又O1Q为小圆半径,即QO1=m,
∴
| 2m2-10m+17 |
如解答图1,连接O2Q,同理可得:n2-10n+17=0 ②
由①,②式可知,m、n是一元二次方程x2-10x+17=0 ③的两个根,
解③得:x=5±2
| 2 |
| 2 |
| 2 |
∵O1(m,m),O2(n,n),
∴d=O1O2=
| (m-n)2+(m-n)2 |
(3)假设存在这样的抛物线,其解析式为y=ax2+bx+c,
 因为开口向下,所以a<0.
因为开口向下,所以a<0.如解答图2,连接PQ.
由相交两圆性质可知,PQ⊥O1O2.
∵P(4,1),Q(1,4),
∴PQ=
| (4-1)2+(1-4)2 |
| 2 |
∴S1=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
又S2=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
∴
| |s1-s2| | ||
|
|12
| ||||
|
∵抛物线过点P(4,1),Q(1,4),
∴
|
|
∴抛物线解析式为:y=ax2-(5a+1)x+5+4a,
令y=0,则有:ax2-(5a+1)x+5+4a=0,
设两根为x1,x2,则有:x1+x2=
| 5a+1 |
| a |
| 5+4a |
| a |
∵在x轴上截得的线段长为1,即|x1-x2|=1,
∴(x1-x2)2=1,∴(x1+x2)2-4x1x2=1,
即(
| 5a+1 |
| a |
| 5+4a |
| a |
解得a=
5±
| ||
| 8 |
∴不存在这样的抛物线.
点评:本题是中考压轴题,综合考查了二次函数的图象与性质、待定系数法、一元二次方程的解法及根与系数关系、两点间的距离公式、相交两圆的性质和圆的切线的性质等知识,涉及的考点众多.第(1)问起点不高;第(2)问可以难住不少考生;若没有(2)的正确计算结果,则第(3)问难以得出正确结论.所以本题难度很大,对考生的综合解题能力要求很高,但同学们只要平时学习打好基础,并将所学知识融会贯通,就能够以不变应万变.

练习册系列答案
相关题目
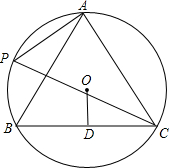 (2012•长沙)如图,A,P,B,C是半径为8的⊙O上的四点,且满足∠BAC=∠APC=60°,
(2012•长沙)如图,A,P,B,C是半径为8的⊙O上的四点,且满足∠BAC=∠APC=60°,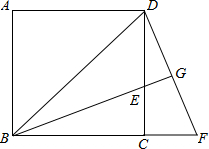 (2012•长沙)如图,已知正方形ABCD中,BE平分∠DBC且交CD边于点E,将△BCE绕点C顺时针旋转到△DCF的位置,并延长BE交DF于点G.
(2012•长沙)如图,已知正方形ABCD中,BE平分∠DBC且交CD边于点E,将△BCE绕点C顺时针旋转到△DCF的位置,并延长BE交DF于点G.
 (2012•长沙)如图,在△ABC中,∠A=45°,∠B=60°,则外角∠ACD=
(2012•长沙)如图,在△ABC中,∠A=45°,∠B=60°,则外角∠ACD=