Question

在平面直角坐标系中，已知两点坐标P₁（x₁，y₁）P₂（x₂，y₂）我们就可以使用两点间距离公式P1P2=

(x1-x2)2+(y1-y 2)2

来求出点P₁与点P₂间的距离．如：已知P₁（-1，2），P₂（0，3），则P1P2=

(-1-0)2+(2-3)2

=

2

．
通过阅读材以上材料，请回答下列问题：
（1）已知点P₁坐标为（-1，3），点P₂坐标为（2，1）
①求P₁P₂=

13

；
②若点Q在x轴上，则△QP₁P₂的周长最小值为

6+

13

．
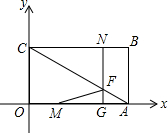
（2）如图，在平面直角坐标系中，四边形OABC为长方形，点A、B的坐标分别为
（4，0）（4，3），动点M、N分别从点O，点B同时出发，以每秒1个单位的速度运动，其中M点沿OA向终点A运动，N点沿BC向终点C运动，过点N作NF⊥BC交AC于F，交AO于G，连结MF．
当两点运动了t秒时：
①直接写出直线AC的解析式：

y=-

3

4

x+3

；
②F点的坐标为（

4-t

，

3

4

t

）；（用含t的代数式表示）
③记△MFA的面积为S，求S与t的函数关系式；（0＜t＜4）；
④当点N运动到终点C点时，在y轴上是否存在点E，使△EAN为等腰三角形？若存在，请直接写出点E的坐标，若不存在，请说明理由．

Answer 1

分析：（1）①利用两点之间的距离公式即可直接求解；
②利用两点之间的距离公式求得OA1和OA2的长度，结合①即可求得三角形的周长；
（2）①利用矩形的性质易求点C的坐标．利用待定系数法可以求得直线AC的方程；
②由平行线分线段成比例得到

FG

OC

=

AG

OA

来求GF的长度，从而易求点F的坐标；
③由三角形的面积公式得到S=

1

2

AM•FG；
④需要分类讨论：AN=AE，NE=AN和AE=NE三种情况．

解答：解：（1）①P₁P₂=

(2+1)2+(1-3)2

=

13

；

②P₁坐标关于x轴的对称点是

P

′ 1

（-1，-3），设直线

P

′ 1

P₂的解析式是y=kx+b（k≠0），
根据题意得：

-k+b=-3 2k+b=1

，
解得：

k=- 4 3 b= 11 3

，
则直线的解析式是：y=-

4

3

x+

11

3

，
在解析式中令y=0，解得：x=

11

4

，
则Q的坐标是：（

11

4

，0），
则QP₁+QP₂=

P

′ 1

P₂=

(2+1)2+(1+4)2

=

9+25

=6，
则△QP₁P₂的周长最小值是：6+

13

；
故填：6+

13

；

（2）①如图，四边形ABCO是矩形，点A、B的坐标分别为（4，0）、（4，3），则C（0，3）．
设直线AC的解析式为：y=kx+b（k≠0），则

4k+b=0 b=3

，
解得，

k=- 3 4 b=3

，
所以直线AC的解析式为：y=-

3

4

x+3；
故填：y=-

3

4

x+3；

②∵NF⊥BC，四边形ABCO是矩形，
∴NG∥OC，BN=AG，
∴

FG

OC

=

AG

OA

，即

FG

3

=

t

4

，
∴FG=

3

4

t，
∴F（4-t，

3

4

t）；

③如图，S=

1

2

AM•FG=

1

2

（4-t）×

3

4

t=-

3

8

t²+

3

2

t（0＜t＜4）；

④∵A（4，0），C（0，3），点N与点C重合，
∴ON=3，OA=4，
∴由勾股定理得到AN=5．
如图，当AN=AE时，易求ON=OE=3，则E₁（0，-3）；
当NE=AN时，OE=5-3=2，则E₂（0，-2）；
当AE=NE时，设E₃（0，t），则（t-3）²=4²+t²
解得，t=

7

6

，
∴E₃（0，

7

6

）；
综上所述，符合条件的点E的坐标分别是：E₁（0，-3），E₂（0，-2），E₃（0，

7

6

）．

点评：本题考查了一次函数综合题．其中涉及到了待定系数法求一次函数解析式，三角形的面积计算，矩形的性质以及等腰三角形的判定与性质．解（3）④题时，要分类讨论．