题目内容
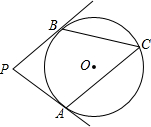
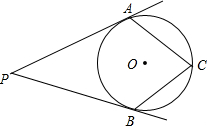 如图,PA、PB切⊙O于点A、B,点C是⊙O上一点,且∠ACB=70°,则∠P=
如图,PA、PB切⊙O于点A、B,点C是⊙O上一点,且∠ACB=70°,则∠P=
- A.30°
- B.40°
- C.50°
- D.60°
B
分析:连接OA和OB,根据切线的性质可得∠PAO=∠PBO=90°,又根据同弧所对的圆心角等于它所对圆周角的2倍,由∠ACB的度数求出∠AOB的度数,在四边形APBO中,根据四边形的内角和为360°,即可求出所求角的度数.
解答: 解:连接OA与OB,由PA与PB为圆O的切线,得到∠PAO=∠PBO=90°,
解:连接OA与OB,由PA与PB为圆O的切线,得到∠PAO=∠PBO=90°,
又 =
= ,∠AOB=2∠ACB=140°,
,∠AOB=2∠ACB=140°,
在四边形APBO中,∠APB=360°-90°-90°-140°=40°.
故选B
点评:此题考查了切线的性质,圆周角定理及四边形的内角和.见了有切线,圆心切点连是此类题解答中运用较突出的一种技巧.本题的解题方法称为“构图建模计算法”,即构造四边形,借助四边形的内角和解决问题.
分析:连接OA和OB,根据切线的性质可得∠PAO=∠PBO=90°,又根据同弧所对的圆心角等于它所对圆周角的2倍,由∠ACB的度数求出∠AOB的度数,在四边形APBO中,根据四边形的内角和为360°,即可求出所求角的度数.
解答:
 解:连接OA与OB,由PA与PB为圆O的切线,得到∠PAO=∠PBO=90°,
解:连接OA与OB,由PA与PB为圆O的切线,得到∠PAO=∠PBO=90°,又
 =
= ,∠AOB=2∠ACB=140°,
,∠AOB=2∠ACB=140°,在四边形APBO中,∠APB=360°-90°-90°-140°=40°.
故选B
点评:此题考查了切线的性质,圆周角定理及四边形的内角和.见了有切线,圆心切点连是此类题解答中运用较突出的一种技巧.本题的解题方法称为“构图建模计算法”,即构造四边形,借助四边形的内角和解决问题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
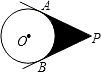 如图,PA、PB切⊙O于A、B两点,若∠APB=60°,⊙O的半径为3,则阴影部分的面积为
如图,PA、PB切⊙O于A、B两点,若∠APB=60°,⊙O的半径为3,则阴影部分的面积为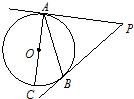 10、如图,PA、PB切⊙O于点A、B,AC是⊙O的直径,且∠BAC=35°,则∠P=
10、如图,PA、PB切⊙O于点A、B,AC是⊙O的直径,且∠BAC=35°,则∠P=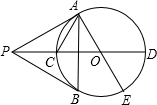 如图,PA、PB切⊙O于A、B,PO及其延长线分别交⊙O于C、D,AE为⊙O的直径,连接AB、AC,下列结论:①
如图,PA、PB切⊙O于A、B,PO及其延长线分别交⊙O于C、D,AE为⊙O的直径,连接AB、AC,下列结论:①
 如图,PA、PB切⊙O于A、B两点,C为优
如图,PA、PB切⊙O于A、B两点,C为优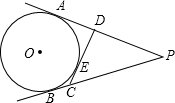 如图,PA、PB切⊙O于A、B两点,CD切⊙O于点E,分别交PA、PB于点C、D.若PA、PB的长是关于x的一元二次方程x2-mx+m-1=0的两个根,求△PCD的周长.
如图,PA、PB切⊙O于A、B两点,CD切⊙O于点E,分别交PA、PB于点C、D.若PA、PB的长是关于x的一元二次方程x2-mx+m-1=0的两个根,求△PCD的周长.