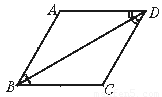
题目内容
平行四边形的一条对角线和一边垂直,且邻边比是1:2,那么平行四边形相邻内角之比是
- A.1:1
- B.1:2
- C.1:3
- D.1:4
B
分析:根据直角三角形的性质可以求得平行四边形的其中一个内角是60°,则平行四边形的与它相邻的内角是120°,从而求得其比值.
解答: 解:如图所示,
解:如图所示,
在直角三角形ABC中,AB:BC=1:2,
∴∠ACB=30°.
∴∠B=60°.
∴∠BAD=120°.
∴∠B:∠BAD=1:2.
故选B.
点评:综合运用了直角三角形的性质和平行四边形的性质.
直角三角形中,如果一条直角边是斜边的一半,则这条直角边所对的角是30°.
分析:根据直角三角形的性质可以求得平行四边形的其中一个内角是60°,则平行四边形的与它相邻的内角是120°,从而求得其比值.
解答:
 解:如图所示,
解:如图所示,在直角三角形ABC中,AB:BC=1:2,
∴∠ACB=30°.
∴∠B=60°.
∴∠BAD=120°.
∴∠B:∠BAD=1:2.
故选B.
点评:综合运用了直角三角形的性质和平行四边形的性质.
直角三角形中,如果一条直角边是斜边的一半,则这条直角边所对的角是30°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
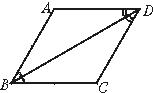 11、若一条对角线平分平行四边形的一组对角,且一边长为a时,如图,其他三边长为
11、若一条对角线平分平行四边形的一组对角,且一边长为a时,如图,其他三边长为