题目内容
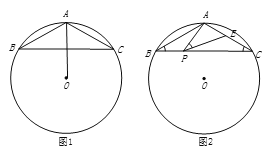
【题目】如图,等腰△ABC内接于半径为5的⊙O,AB=AC,BC=8.
(1)如图1,连结OA.
①求证:OA⊥BC;
②求腰AB的长.
(2)如图2,点P是边BC上的动点(不与点B,C重合),∠APE=∠B=∠C,PE交AC于E.
①求线段CE的最大值;
②当AP=PC时,求BP的长.
【答案】(1)①证明见解析;②2![]() ;(2)①CE的最大值为
;(2)①CE的最大值为![]() ;②BP=
;②BP=![]() .
.
【解析】
(1)①由AB=AC,得![]() ,故OA⊥BC;②连结OB,设OA交BC于D.由垂径定理可得
,故OA⊥BC;②连结OB,设OA交BC于D.由垂径定理可得
BD=CD=![]() BC=4.再利用勾股定理可得AB=
BC=4.再利用勾股定理可得AB=![]() .(2)先证△ABP∽△PCE,得
.(2)先证△ABP∽△PCE,得![]() .设BP=x,CE=y,则PC=8-x,可得
.设BP=x,CE=y,则PC=8-x,可得![]() ,可得y=
,可得y=![]() ,可求出函数的最值;②证△APC∽△BAC,得
,可求出函数的最值;②证△APC∽△BAC,得![]() ,可得PC=
,可得PC=![]() ,故BP=BC-PC.
,故BP=BC-PC.
解:(1)①∵AB=AC,
∴![]() ,
,
∴OA⊥BC
②连结OB,设OA交BC于D.
∵OA⊥BC ,
∴BD=CD=![]() BC=4.
BC=4.
∴OD=![]() =3,
=3,
∴AD=OA-OD=5-3=2,
∴AB=![]() .
.
(2)①∵∠APE=∠B=∠C,
∴∠BAP+∠APB=∠APB+∠CPE,
∴∠BAP=∠CPE,
∴△ABP∽△PCE,
∴![]() .
.
设BP=x,CE=y,则PC=8-x,
∴![]() ,
,
∴y=![]()
∴当x=4时,ymax=![]() ,即CE的最大值为
,即CE的最大值为![]()
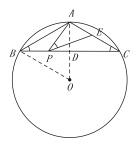
②∵AP=PC,
∴∠PAC=∠C=∠B,
∴△APC∽△BAC,
∴![]() ,
,
∴![]() ,
,
∴PC=![]() ,
,
∴BP=BC-PC=![]()

练习册系列答案
相关题目