题目内容
若实数a满足a3+a2-3a+2=
-
-
，则a+
=
| 3 |
| a |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| a |
2或-3
2或-3
分析：首先把等式移项a3+a2-3a+2-
+
+
=0，然后分组，分别利用立方和公式、完全平方公式、分解因式得到（a+
）（a+
+3）（a+
-2）=0，由此即可求出结果．
| 3 |
| a |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
解答：解：∵实数a满足a3+a2-3a+2=
-
-
，
∴a3+a2-3a+2-
+
+
=0，
∴a3+
+a2+
+2-3（a+
）=0，
（a+
）（a2-1+
）+（a+
）2-3（a+
）=0，
（a+
）（a2-1+
+a+
-3）=0，
∴（a+
）[（a+
）2+（a+
）-6]=0，
∴（a+
）（a+
+3）（a+
-2）=0，
而a+
≠0，
∴a+
+3=0，或a+
-2=0，
∴a+
=-3或2．
故答案为：-3或2．
| 3 |
| a |
| 1 |
| a2 |
| 1 |
| a3 |
∴a3+a2-3a+2-
| 3 |
| a |
| 1 |
| a2 |
| 1 |
| a3 |
∴a3+
| 1 |
| a3 |
| 1 |
| a2 |
| 1 |
| a |
（a+
| 1 |
| a |
| 1 |
| a2 |
| 1 |
| a |
| 1 |
| a |
（a+
| 1 |
| a |
| 1 |
| a2 |
| 1 |
| a |
∴（a+
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
∴（a+
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
而a+
| 1 |
| a |
∴a+
| 1 |
| a |
| 1 |
| a |
∴a+
| 1 |
| a |
故答案为：-3或2．
点评：此题主要考查了立方差公式、完全平方公式及利用分组法分解因式，解题的关键通过分组能够分解因式，也利用了整体代值的思想，题目比较难，对于学生的代数变形的能力要求比较高．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
-
-
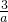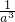，则a+
=________