题目内容
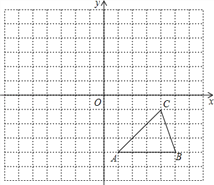
【题目】将长方形ABCD按如图所示沿EF所在直线折叠,点C落在AD上的点C′处,点D落在点D′处.
(1)求证:△EFC′是等腰三角形.
(2)如果∠1=65°,求∠2的度数.

【答案】(1)证明见解析;(2)∠2=40°.
【解析】
(1)根据折叠的性质得到∠EFC′=∠1,由平行线的性质得到∠1=∠FBC′,等量代换得到∠EFC′=′FEC′,根据等腰三角形的判定定理即可得到结论;
(2)根据折叠的性质和已知条件得到∠EC′F=180°﹣∠FEC′﹣∠EFC′=180°﹣65°=65°=50°,由于∠D′C′F=∠2+∠EC′F=∠C=90°即可得到结论.
(1)证明:四边形EFC′D′是将长方形ABCD中的四边形CDEF沿EF所在直线折叠得到的,
∴∠EFC′=∠1,
∵AD∥BC,
∴∠1=∠FBC′,
∴∠EFC′=′FEC′,
∴FC′=EC′,
∴△EFC′是等腰三角形;
(2)解:∵∠1=∠FEC′=∠EFC′,∠1=65°,
∴∠EC′F=180°﹣∠FEC′﹣∠EFC′=180°﹣65°=65°=50°,
∵∠D′C′F=∠2+∠EC′F=∠C=90°,
∴∠2=90°﹣∠EC′F=40°,
∴∠2=40°.

【题目】2019 年 3 月 31 日,南京地铁新的价格方案正式实施,实行消费累进优惠.普通成人每月持卡乘坐地铁,当消费累计金额不超过 150 元时,每次乘坐地铁的票价打 9.5 折;当消费累计金 额超过 150 元时,达到规定的消费累计金额后的乘次,票价所打折扣如下表所示:
消费累计金额 | 折扣 |
| 9折 |
| 8折 |
| 9.5折 |
小明上、下班每次乘坐的地铁单程票价为 10元,2019年 4月份他上、下班持卡共乘坐了 40次.
(1)填表:
第1 次 | 第2 次 | … | 第15次 | 第16次 | 第17次 | … | |
消费累计 金额(元) | 9.5 | 19 | … | 142.5 | 152 | … |
span>
(2)小明当月第几次乘车后,消费累计金额超过 20元?(用一元一次不等式解决问题)
(3)小明 4月份上、下班持卡乘坐地铁的消费累计金额为 元.