题目内容
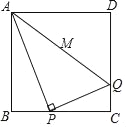
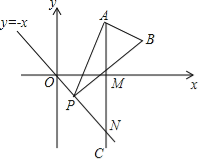
【题目】如图,已知点A是第一象限内横坐标为![]() 的一个定点,AC⊥x轴于点M,交直线y=-x于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动.求当点P从点O运动到点N时,点B运动的路径长是 .
的一个定点,AC⊥x轴于点M,交直线y=-x于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动.求当点P从点O运动到点N时,点B运动的路径长是 .
【答案】![]() .
.
【解析】
(1)首先,需要证明线段B0Bn就是点B运动的路径(或轨迹),如答图②所示.利用相似三角形可以证明;
(2)其次,如答图①所示,利用相似三角形△AB0Bn∽△AON,求出线段B0Bn的长度,即点B运动的路径长.
由题意可知,OM=![]() ,点N在直线y=-x上,AC⊥x轴于点M,则△OMN为等腰直角三角形,
,点N在直线y=-x上,AC⊥x轴于点M,则△OMN为等腰直角三角形,
∴ ON=![]() .
.
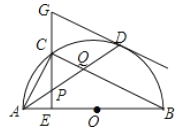
如答图①所示,
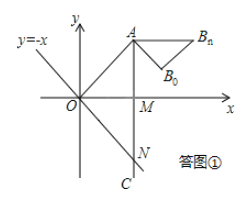
设动点P在O点(起点)时,点B的位置为B0,动点P在N点(起点)时,点B的位置为Bn,连接B0Bn.
∵AO⊥AB0,AN⊥ABn,
∴∠OAC=∠B0ABn.
又∵AB0=AOtan30°,ABn=ANtan30°,
∴AB0:AO=ABn:AN=tan30°.
∴△AB0Bn∽△AON,且相似比为tan30°.
∴B0Bn=ONtan30°=![]() .
.
现在来证明线段B0Bn就是点B运动的路径(或轨迹):
如答图②所示,
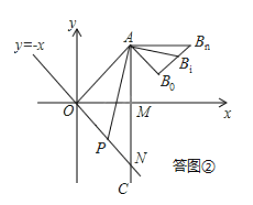
当点P运动至ON上的任一点时,设其对应的点B为Bi,连接AP,ABi,B0Bi.
∵AO⊥AB0,AP⊥ABi,
∴∠OAP=∠B0ABi.
又∵AB0=AOtan30°,ABi=APtan30°,
∴AB0:AO=ABi:AP.
∴△AB0Bi∽△AOP,
∴∠AB0Bi=∠AOP.
又∵△AB0Bn∽△AON,
∴∠AB0Bn=∠AOP.
∴∠AB0Bi=∠AB0Bn.
∴点Bi在线段B0Bn上,即线段B0Bn就是点B运动的路径(或轨迹).
综上所述,点B运动的路径(或轨迹)是线段B0Bn,其长度为![]() .
.

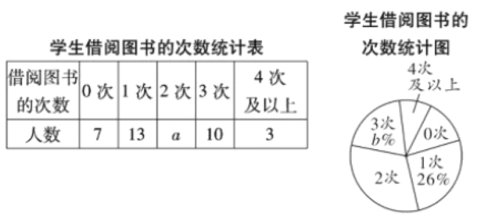
【题目】立定跳远是体育中考选考项目之一,体育课上老师记录了某同学的一组立定跳远成绩如表:
成绩(m) | 2.3 | 2.4 | 2.5 | 2.4 | 2.4 |
则下列关于这组数据的说法,正确的是( )
A.众数是2.3B.平均数是2.4
C.中位数是2.5D.方差是0.01
【题目】某校八年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作.已知该水果的进价为8元/千克,下面是他们在活动结束后的对话.
小丽:如果以10元/千克的价格销售,那么每天可售出300千克.
小强:如果每千克的利润为3元,那么每天可售出250千克.
小红:如果以13元/千克的价格销售,那么每天可获取利润750元.
【利润=(销售价-进价)![]() 销售量】
销售量】
(1)请根据他们的对话填写下表:
销售单价x(元/kg) | 10 | 11 | 13 |
销售量y(kg) |
(2)请你根据表格中的信息判断每天的销售量y(千克)与销售单价x(元)之间存在怎样的函数关系.并求y(千克)与x(元)(x>0)的函数关系式;
(3)设该超市销售这种水果每天获取的利润为W元,求W与x的函数关系式.当销售单价为何值时,每天可获得的利润最大?最大利润是多少元?