��Ŀ����
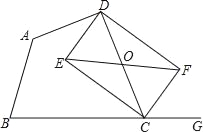
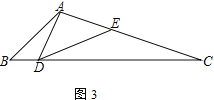
����Ŀ����֪��ƽ��ֱ������ϵ�У���A(��2��0)��B(0��3)����PΪ�ڶ�������һ��
(1) ��ͼ�����߶�AB�Ƶ�P��ת180�����߶�CD����A���C��Ӧ���Ի���ͼ����
(2) ��(1)�еõ��ĵ�C��Dǡ����ͬһ������������![]() ��ͼ���ϣ�����ֱ��BC�Ľ���ʽ��
��ͼ���ϣ�����ֱ��BC�Ľ���ʽ��
(3) ����Q(m��n)Ϊ��������һ�㣬���߶�AB�Ƶ�Q˳ʱ����ת90������E��F������E��Fǡ����ͬһ��������������ͼ���ϣ���ֱ��д��m��n֮��Ĺ�ϵʽ__________________��
���𰸡�m����5n
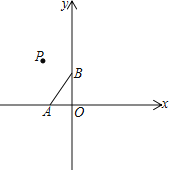
��������������(1)�ҳ���A,B���ڵ�P�ĶԳƵ㣬���Ӽ���.
![]() ��P(m��n)����C(2��2m��2n)��D(2m��2n��3)�����ݵ�C��Dǡ����ͬһ������������
��P(m��n)����C(2��2m��2n)��D(2m��2n��3)�����ݵ�C��Dǡ����ͬһ������������![]() ��ͼ���ϣ���2n(2��2m)��2m(2n��3)���õ�2n��-3m����ֱ��BC�Ľ���ʽΪ��y��kx��3������C(2��2m��-3m)����y��kx��3���������һ�κ�������ʽ.
��ͼ���ϣ���2n(2��2m)��2m(2n��3)���õ�2n��-3m����ֱ��BC�Ľ���ʽΪ��y��kx��3������C(2��2m��-3m)����y��kx��3���������һ�κ�������ʽ.
![]() ������ת���������E(m��n��m��n��2)��F(m��3��n��n��m),����
������ת���������E(m��n��m��n��2)��F(m��3��n��n��m),����![]() �������m��n֮��Ĺ�ϵʽ.
�������m��n֮��Ĺ�ϵʽ.
��⣺(1)��ͼ��ʾ��
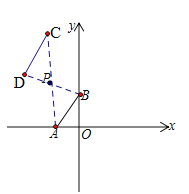
(2) ��P(m��n)����C(2��2m��2n)��D(2m��2n��3)
�ߵ�C��Dǡ����ͬһ������������![]() ��ͼ����
��ͼ����
��2n(2��2m)��2m(2n��3)����2n��-3m��
��ֱ��BC�Ľ���ʽΪ��y��kx��3
��C(2��2m����3m)����y��kx��3����
![]() �����
�����![]() ��
��![]()
(3) ������ֱ�ã�E(m��n��m��n��2)��F(m��3��n��n��m)
��(m��n)(m��n��2)��(m��3��n)(n��m)��
������m��-5n.

 �������ͬ����ϰϵ�д�
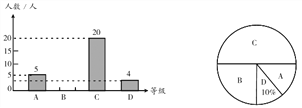
�������ͬ����ϰϵ�д�����Ŀ��Ϊ������Ӧ�����ﴫͳ�Ļ����ĺ��٣�ijѧУ��֯ȫУ1200��ѧ�����о���ʫ���ж�������ڻ֮��ٰ쾭��ʫ�ʴ�����Ϊ�˽Ȿ��ϵ�л�ij���Ч����ѧУ��ί�ڻ����֮���������ȡ40��ѧ��������һ��ʫ���б������������ݵ��������Ƴɵ�ͳ��ͼ��ͼ��ʾ.

����������һ���£��ٴγ���ⲿ��ѧ����һ��ʫ���б������������Ƴ�ͳ�Ʊ����£�
һ��ʫ���б����� | 3�� | 4�� | 5�� | 6�� | 7�� | 8�� |
���� | 1 | 3 | 5 | 6 | 10 | 15 |
����ݵ������Ϣ
��1��������֮��ѧ����һ��ʫ���б�����������λ����
��2�����ƴ�����һ���¸�Уѧ��һ��ʫ���б�6�ף���6�ף����ϵ�������
��3��ѡ���ʵ���ͳ���������ٴ�������ͬ�ĽǶȷ������ε����������ݣ����۸�У����ʫ���б�ϵ�л��Ч��.