题目内容
【题目】如图,在△ABC中,AB=AC,D为BC中点,四边形ABDE是平行四边形,AC、DE相交于点O. 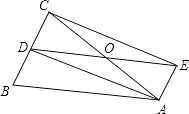
(1)求证:四边形ADCE是矩形.
(2)若∠AOE=60°,AE=4,求矩形ADCE对角线的长.
【答案】
(1)证明:∵四边形ABDE是平行四边形,
∴AB=DE,
又∵AB=AC,
∴DE=AC.
∵AB=AC,D为BC中点,
∴∠ADC=90°,
又∵D为BC中点,
∴CD=BD.
∴CD∥AE,CD=AE.
∴四边形AECD是平行四边形,
又∴∠ADC=90°,
∴四边形ADCE是矩形.
(2)解:∵四边形ADCE是矩形,
∴AO=EO,
∴△AOE为等边三角形,
∴AO=4,
故AC=8.
【解析】(1)根据四边形ABDE是平行四边形和AB=AC,推出AD和DE相等且互相平分,即可推出四边形ADCE是矩形.(2)根据∠AOE=60°和矩形的对角线相等且互相平分,得出△AOE为等边三角形,即可求出AO的长,从而得到矩形ADCE对角线的长.
【考点精析】利用等腰三角形的性质和平行四边形的性质对题目进行判断即可得到答案,需要熟知等腰三角形的两个底角相等(简称:等边对等角);平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.

【题目】我市某西瓜产地组织40辆汽车装运完A,B,C三种西瓜共200吨到外地销售.按计划,40辆汽车都要装运,每辆汽车只能装运同一种西瓜,且必须装满.根据下表提供的信息,解答以下问题:
西瓜种类 | A | B | C |
每辆汽车运载量(吨) | 4 | 5 | 6 |
每吨西瓜获利(百元) | 16 | 10 | 12 |
(1)设装运A种西瓜的车辆数为x辆,装运B种西瓜的车辆数为y辆,求y与x的函数关系式;
(2)如果装运每种西瓜的车辆数都不少于10辆,那么车辆的安排方案有几种?并写出每种安排方案;
(3)若要是此次销售获利达到预期利润25万元,应采取怎样的车辆安排方案?
【题目】甲、乙、丙三位运动员在相同条件下各射靶10次,每次射靶的成绩如下:
甲:9,10,8,5,7,8,10,8,8,7;
乙:5,7,8,7,8,9,7,9,10,10;
丙:7,6,8,5,4,7,6,3,9,5.
(1)根据以上数据完成下表:
平均数 | 中位数 | 方差 | |
甲 | 8 | 8 | |
乙 | 8 | 8 | 2.2 |
丙 | 6 | 3 |
(2)依据表中数据分析,哪位运动员的成绩最稳定,并简要说明理由;
(3)比赛时三人依次出场,顺序由抽签方式决定.求甲、乙相邻出场的概率.