题目内容
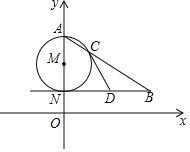
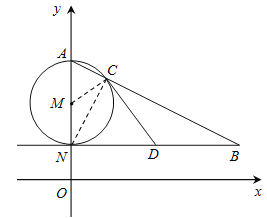
【题目】如图，AN是⊙M的直径，NB∥x轴，AB交⊙M于点C．
（1）若点A（0，6），N（0，2），∠ABN=30°，求点B的坐标；
（2）若D为线段NB的中点，求证：直线CD是⊙M的切线．
【答案】(1) B（
，2）．(2)证明见解析.
【解析】
试题分析：（1）在Rt△ABN中，求出AN、AB即可解决问题；
（2）连接MC，NC．只要证明∠MCD=90°即可
试题解析：（1）∵A的坐标为（0，6），N（0，2），
∴AN=4，
∵∠ABN=30°，∠ANB=90°，
∴AB=2AN=8，
∴由勾股定理可知：NB=
，
∴B（，2）．
（2）连接MC，NC
∵AN是⊙M的直径，
∴∠ACN=90°，
∴∠NCB=90°，
在Rt△NCB中，D为NB的中点，
∴CD=
NB=ND，
∴∠CND=∠NCD，
∵MC=MN，
∴∠MCN=∠MNC，
∵∠MNC+∠CND=90°，
∴∠MCN+∠NCD=90°，
即MC⊥CD．
∴直线CD是⊙M的切线．
练习册系列答案
相关题目
