题目内容
【题目】如图,已知正方形ABCD中,点E在边DC上,DE=2,EC=1.把△ADE绕点A旋转90°,点E的对应点为点F,则F、C两点的距离为___________.
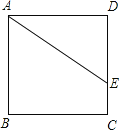
【答案】5或![]()
【解析】
根据正方形的性质可得AB=AD,∠ABC=∠D=90°,再根据旋转的性质可得AF=AE,然后利用“HL”证明Rt△ABF和Rt△ADE全等,根据全等三角形对应边相等可得BF=DE,再求出正方形的边长为3,然后分两种情况讨论求解.
如图,
在正方形ABCD中,AB=AD,∠ABC=∠D=90°,
由旋转的性质得,AF=AE,
在Rt△ABF和Rt△ADE中,
![]() ,
,
∴Rt△ABF≌Rt△ADE(HL),
∴BF=DE=2,
∵DE=2,EC=1,
∴正方形的边长为2+1=3,
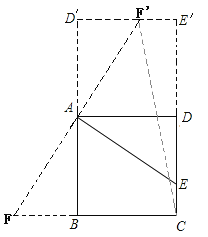
①点F在线段CB延长线上时,FC=BF+BC=3+2=5;
②当线段AE逆时针旋转90°时,延长CD、D’F’交于点E’,
由勾股定理得,F’C=![]() .
.
故答案为:5或![]() .
.

练习册系列答案
相关题目