题目内容
【题目】综合题,如图,正方形ABCD。
(1)请在图①中作两条直线,使它们将正方形ABCD的面积三等分;
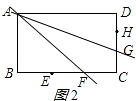
(2)如图②,在矩形ABCD中,AB=6,BC=9,在图②中过顶点A作两条直线,使它们将矩形ABCD的面积三等分,井说明理由;
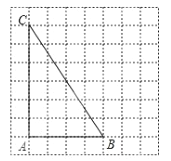
(3)如图③,农博园有一块不规则的五边形ABCDE空地,其中AB∥CD、AE∥BC,AB=AC=100米,AE=160米,BC=120米,CD=62.5米,根据视觉效果和花期特点,农博园设计部门想在这片空地种上等面积的三种不同的花,要求从入口A点处修两条笔直的小路(小路的面积忽略不计)方便游客赏花,两条小路将这块地面积三等分.请通过计算画图说明其设计部们能否实现,若能实现请确定小路尽头的位置.
【答案】
(1)解:在正方形ABCD中,
分别取BC、AD的三等分点E、F、G、H,
作直线EG、FH,
即把正方形ABCD的面积三等分;
如图1所示:

(2)解:在矩形ABCD中,
分别取BC、CD的三等分点E、F、G、H,
作直线AF、AG,
即把正方形ABCD的面积三等分;
如图2所示;
问题解决
(3)解:作AF⊥BC于F,延长CD交AE于G,如图3所示:
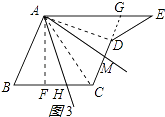
∵AB=AC,
∴BF=CF= ![]() BC=60米
BC=60米
∴AF= ![]() =
= ![]() =80(米),
=80(米),
∵AB∥CD、AE∥BC,
∴四边形ABCG是平行四边形,
∴平行四边形ABCG的面积=BCAF=120×80=9600(平方米),
∴CG=AB=100米,AG=BC=120米,DG=CG﹣CD=100﹣62.5=37.5(米),GE=AE﹣AG=160﹣120=40(米),
∴ ![]() =
= ![]() =
= ![]() ,
,
∵AF=80米,
∴根据平行线截得的线段成比例:△DGE的GE边上的高为:30米,
∴S△DGE= ![]() ×30×40=600(平方米),
×30×40=600(平方米),
五边形ABCDE的面积=平行四边形ABCG的面积+S△DGE=9600+600=10200(平方米),
则三等分面积为3400平方米,
设在BC边上截取点H,使△ABH的面积为3400平方米,
即 ![]() AFBH=3400,
AFBH=3400, ![]() ×80BH=3400,
×80BH=3400,
解得:BH=85(米),
∵S△ABC= ![]() BCAF=
BCAF= ![]() ×120×80=4800(平方米),
×120×80=4800(平方米),
∴S△ACH=S△ABC﹣S△ABH=4800﹣3400=1400(平方米),
∵S△ACD=480× ![]() =300(平方米),140+200=340(平方米),
=300(平方米),140+200=340(平方米),
∴在CD上取CD的第二个三等分点M,CM= ![]() CD=
CD= ![]() (米),
(米),
∴直线AH、AM就可把五边形面积三等分,
∴H、M点就是小路尽头的位置.
【解析】(1)分别取BC、AD的三等分点E、F、G、H,即可,也可以取AD的三等分点G、H。过点G、H分别作BC的垂线;(2)分别取BC、CD的三等分点E、F、G、H,连接AF、AG,即可;(3)此小题综合性强,抓住已知条件AB∥CD、AE∥BC,所以延长延长CD交AE于G,构造平行四边形ABCG,已知AB=AC=100米,得等腰三角形,根据等腰三角形三线合一的性质,过点A作AF⊥BC于F,求得AF的长,就可以求得平行四边形ABCG的面积。易得DG:CD=![]() ,由AF=80,可以得到△DGE的GE边上的高为:
,由AF=80,可以得到△DGE的GE边上的高为:![]()
![]() 80=30米,得到△DGE的面积,从而可求得五边形ABCDE的面积为10200(平方米),要将此五边形的面积三等分,就得出三等分图形的面积,在△ABC的BC边取一点H,使△ABH的面积为3400,可以求得BH的长。再求出△ACH的面积,再求出M点的位置,作出直线即可。
80=30米,得到△DGE的面积,从而可求得五边形ABCDE的面积为10200(平方米),要将此五边形的面积三等分,就得出三等分图形的面积,在△ABC的BC边取一点H,使△ABH的面积为3400,可以求得BH的长。再求出△ACH的面积,再求出M点的位置,作出直线即可。
【考点精析】掌握平行四边形的性质和正方形的性质是解答本题的根本,需要知道平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.