题目内容
某公司为了扩大经营,决定购进6台机器用于生产某种零件.现有甲、乙两种机器供选择,其中每种机器的价格和每台机器日生产零件的数量如下表所示.经过预算,本次购买机器所耗资金不能超过34万元.
(1)按该公司要求可以有几种购买方案?
(2)若该公司购进的6台机器的日生产能力不能低于190个,那么为了节约资金应选择哪种方案?
| | 甲 | 乙 |
| 价格(万元/台) | 7 | 5 |
| 每台日产量(个) | 50 | 30 |
(2)若该公司购进的6台机器的日生产能力不能低于190个,那么为了节约资金应选择哪种方案?
(1)三种购买方案:
方案一:不购买甲种机器,购买乙种机器6台;
方案二:购买甲种机器1台,购买乙种机器5台;
方案三:购买甲种机器2台,购买乙种机器4台;
(2)方案二.
方案一:不购买甲种机器,购买乙种机器6台;
方案二:购买甲种机器1台,购买乙种机器5台;
方案三:购买甲种机器2台,购买乙种机器4台;
(2)方案二.
试题分析:(1)设购买甲种机器x台,则购买乙种机器(6-x)台,根据本次购买机器所耗资金不能超过34万元即可列不等式求得结果;
(2)分别计算出这三种方案的所耗资金及生产能力,再比较即可得到结果.
(1)设购买甲种机器x台,则购买乙种机器(6-x)台,由题意得
7x+5(6-x)≤34
解得x≤2
∵x为非负整数
∴x取0、1、2
∴该公司按要求可以有以下三种购买方案:
方案一:不购买甲种机器,购买乙种机器6台;
方案二:购买甲种机器1台,购买乙种机器5台;
方案三:购买甲种机器2台,购买乙种机器4台;
(2)按方案一购买机器,所耗资金为30万元,新购买机器日生产量为180个;
按方案二购买机器,所耗资金为1×7+5×5=32万元;
新购买机器日生产量为1×50+5×30=200个;
按方案三购买机器,所耗资金为2×7+4×5=34万元;
新购买机器日生产量为2×50+4×30=220个.
∵选择方案二既能达到生产能力不低于190个的要求,又比方案三节约2万元资金,
故应选择方案二.
点评:解答本题的关键是读懂题意,找到不等关系,正确列出不等式,再求解,注意实际问题中的解往往取正整数.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
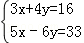
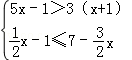 并把解集表示在数轴上
并把解集表示在数轴上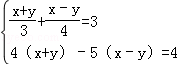
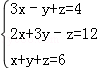 .
. 时,不等式(
时,不等式(
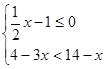 并将其解集在数轴上表示出来。
并将其解集在数轴上表示出来。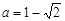 时,求
时,求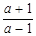 -
-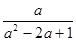 ÷
÷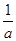 的值.
的值.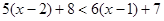
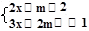 无解,则 m 的取值范围 .
无解,则 m 的取值范围 .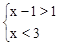 的解集为 .
的解集为 .