Question

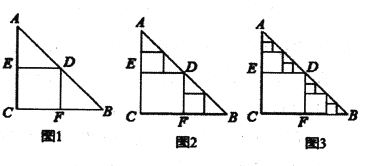
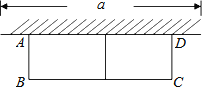
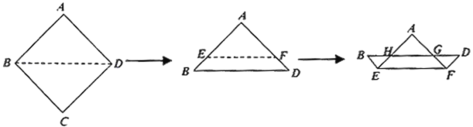
【题目】如图，将一张正方形纸片，依次沿着折痕，（其中）向上翻折两次，形成“小船”的图样．若，四边形与的周长差为，则正方形的周长为______．

Answer 1

【答案】16

【解析】

由正方形的性质得出△ABD是等腰直角三角形，由EF∥BD，得出△AEF是等腰直角三角形，由折叠的性质得△AHG是等腰直角三角形，△BEH与△DFG是全等的等腰直角三角形，则GF=DF=BE=EH=1，设AB=x，则BD=x，EF=（x-1），AH=AG=x-2，HG=（x-2），由四边形BEFD与△AHG的周长差为5-2列出方程解得x=4，即可得出结果．

∵四边形ABCD是正方形，

∴△ABD是等腰直角三角形，

∵EF∥BD，

∴△AEF是等腰直角三角形，

由折叠的性质得：△AHG是等腰直角三角形，△BEH与△DFG是全等的等腰直角三角形，

∴GF=DF=BE=EH=1，

设AB=x，

则BD=x，EF=（x-1），AH=AG=x-2，HG=（x-2），

∵四边形BEFD与△AHG的周长差为5-2，

∴x+（x-1）+2-[2（x-2）+（x-2）]=5-2，

解得：x=4，

∴正方形ABCD的周长为：4×4=16，

故答案为：16．