��Ŀ����
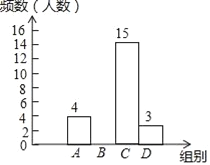
����Ŀ��Ϊ�ḻѧ����У���ijУ���С��밮ͬ�С����б�����������������ͬѧ�ijɼ������Ƴ����²�������ͳ��ͼ���������ͼ���е���Ϣ����������⣮
��� | �ɼ�x���֣� | Ƶ���������� |
A | 8.0��x��8.5 | a |
B | 8.5��x��9.0 | 8 |
C | 9.0��x��9.5 | 15 |
D | 9.5��x��10 | 3 |
��1��ͼ��a=�� ������α����ɼ������������� ���飻
��2���벹ȫƵ���ֲ�ֱ��ͼ��
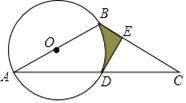
��3��ѧУ����ѡ�ɱ��α����ɼ���õ�3�˲μ�ȫ����ѧ�����б�������Ϊ����ѡ������2����ɫ��1����ɫ���ºͺ�ɫ����ɫ����ɫ�Ŀ��Ӹ�1����С����ѡ�����������ѡȡһ�����º�һ�����Ӵ����һ���·������û���״ͼ�����б���������ºͿ��Ӵ���ɲ�ͬ��ɫ�ĸ��ʣ�
���𰸡�1��4,C����2��Ƶ���ֲ�ֱ��ͼ����������3��![]() .
.
������������: ��1��������ͼ�ɵ�a��ֵ�����������Ķ��弰Ƶ���ֲ����ɵô𰸣���2������Ƶ���ֲ����ó�B���Ƶ�����ɲ�ȫ����ͼ����3���б����ó����еȿ��ܽ�����ٸ��ݸ��ʹ�ʽ�ɵô𰸣�
�������:��1��������ͳ��ͼ��֪��a=4����Ƶ���ֲ�ֱ��ͼ��֪��α����ɼ�����������C�飬
�ʴ�Ϊ��4��C��
��2����ȫƵ���ֲ�ֱ��ͼ���£�

��3����������ɫ���·ֱ��Ϊ��1����2��������״ͼ�����б��� �ã�
��1 | ��2 | �� | |
�� | ����1���ڣ� | ����2���ڣ� | �������ڣ� |
�� | ����1������ | ����2������ | ���������� |
�� | ����1���ף� | ����2���ף� | �������ף� |
����״ͼ��������Կ��������п��ܳ��ֵĽ������9�֣���Щ������ֵĿ�������ȣ��������ºͿ��Ӵ���ɲ�ͬ��ɫ�Ľ����6�֣�
��P�����ºͿ��Ӵ���ɲ�ͬ��ɫ��=![]() ��
��

 �п������п��Ծ����ϵ�д�
�п������п��Ծ����ϵ�д�����Ŀ������ij���ճ�Ϊ��ϱ������ˣ������һ��ɱ�Ϊ20Ԫ�M���Ĺ���ƷͶ���г������������������飬�õ��������ݣ�
���۵���x��Ԫ/���� | �� | 30 | 40 | 50 | 60 | �� |
ÿ��������y������ | �� | 500 | 400 | 300 | 200 | �� |
��1�����ϱ���x��y�ĸ����Ӧֵ��Ϊ������꣬�������ƽ��ֱ������ϵ�������Ӧ�ĵ㣬����y��x�ĺ�����ϵ�������������ϵʽ��
��2�������۵��۶�Ϊ����ʱ�����ճ������ù���Ʒÿ���õ����������������Ƕ��٣�������=�����ܼ۩��ɱ��ܼۣ�
��3��������۲��Ź涨���ù���Ʒ���۵�����߲��ܳ���45Ԫ/������ô���۵��۶�Ϊ����ʱ�����ճ������ù���Ʒÿ���õ��������