题目内容
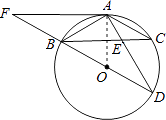
【题目】如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=2,ED=4, 
(1)求证:△ABE∽△ADB;
(2)求AB的长;
(3)延长DB到F,使得BF=BO,连接FA,试判断直线FA与⊙O的位置关系,并说明理由.
【答案】
(1))证明:∵AB=AC,
∴∠ABC=∠C(等边对等角),
∵∠C=∠D(同弧所对的圆周角相等),
∴∠ABC=∠D(等量代换),
又∵∠BAE=∠DAB,
∴△ABE∽△ADB,
(2)解:∵△ABE∽△ADB,
∴ ![]() ,
,
∴AB2=ADAE=(AE+ED)AE=(2+4)×2=12,
∴AB=2 ![]() .
.
(3)解:直线FA与⊙O相切,理由如下:
连接OA,∵BD为⊙O的直径,
∴∠BAD=90°,
∴ ![]() =4
=4 ![]()
BF=BO= ![]() ,
,
∵AB=2 ![]() ,
,
∴BF=BO=AB,
∴∠OAF=90°,
∴OA⊥AF,
∵AO是圆的半径,
∴直线FA与⊙O相切.
【解析】(1)根据AB=AC,可得∠ABC=∠C,利用等量代换可得∠ABC=∠D然后即可证明△ABE∽△ADB.(2)根据△ABE∽△ADB,利用其对应边成比例,将已知数值代入即可求得AB的长.(3)连接OA,根据BD为⊙O的直径可得∠BAD=90°,利用勾股定理求得BD,然后再求证∠OAF=90°即可.
【考点精析】本题主要考查了勾股定理的概念和圆周角定理的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能正确解答此题.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目