题目内容
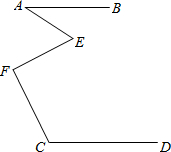
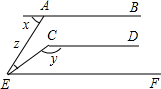
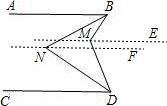
如图,AB∥CD,BN、DN分别平分∠ABM、∠MDC,试问∠BMD与∠BND之间的数量关系如何?证明你的结论.

∠BMD=2∠BND.理由如下:
过点M作直线ME∥AB,过点N作直线NF∥AB,(3分)
又∵AB∥CD,
∴ME∥CD,NF∥CD(平行于同一直线的两直线互相平行),
∴∠ABM=∠BME,∠CDM=∠DME(两直线平行,内错角相等),
∴∠BMD=∠BME+∠DME=∠ABM+∠CDM.
同理可得:∠BND=∠ABN+∠CDN.
∵BN,DN分别平分∠ABM,∠MDC,
∴∠ABM=2∠ABN,∠CDM=2∠CDN(角平分线定义)
∴∠BMD=2∠BND.
过点M作直线ME∥AB,过点N作直线NF∥AB,(3分)
又∵AB∥CD,
∴ME∥CD,NF∥CD(平行于同一直线的两直线互相平行),
∴∠ABM=∠BME,∠CDM=∠DME(两直线平行,内错角相等),
∴∠BMD=∠BME+∠DME=∠ABM+∠CDM.
同理可得:∠BND=∠ABN+∠CDN.
∵BN,DN分别平分∠ABM,∠MDC,
∴∠ABM=2∠ABN,∠CDM=2∠CDN(角平分线定义)
∴∠BMD=2∠BND.


练习册系列答案
相关题目