��Ŀ����
����Ŀ�������龳��
����֪����������ƽ���߱�������ֱ�����أ�ͬλ����ȣ��ڴ�����ȣ�ͬ���ڽǻ�������������ijЩ̽����������ͨ��������ƽ������������ת�������ã�
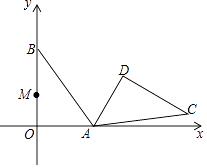
��֪���ǰ�![]() �У�
��![]() ��������
��������![]() ��
��![]() ��
��
�����̽��
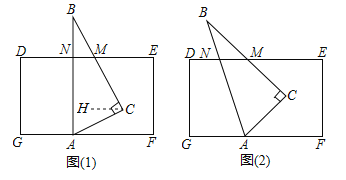
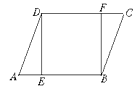
��1����ͼ��1�����������ǰ�![]() �Ķ���
�Ķ���![]() ���ڳ����εı�
���ڳ����εı�![]() �ϣ�
�ϣ�![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() �Ķ�����
�Ķ�����
����![]() ��
��![]() ������
������![]() ���Ӷ���
���Ӷ���![]() ���Ӷ��������
���Ӷ��������![]() �Ķ�����
�Ķ�����
�ɷ����ã�����ֱ��д����![]() �Ķ���Ϊ____________��
�Ķ���Ϊ____________��![]() �Ķ���Ϊ___________��
�Ķ���Ϊ___________��
�����̽��
��2���������ǰ�![]() ��ͼ��2����ʾ��ʽ�ڷţ�
��ͼ��2����ʾ��ʽ�ڷţ�![]() ��
��![]() ����ֱ�����������д��
����ֱ�����������д��![]() ��
��![]() ��������ϵ����˵�����ɣ�
��������ϵ����˵�����ɣ�
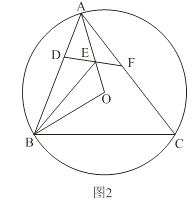
���𰸡���1��30����60������2����CAF+��EMC=90�������ɼ�����
��������
��1�����á�CAF=��BAF-��BAC�����CAF���������EMC����ת������MCH������
��2������C��CH��GF���õ�CH��DE����CAF���EMCת������ACH�͡�MCH�У��Ӷ����֡�CAF����EMC���ACB��������ϵ��
��1������C��CH��GF������CH��DE��
���ԡ�CAF=��HCA����EMC=��MCH��
�ߡ�BAF=90����
���CAF=90��-60��=30����
��MCH=90��-��HCA=60����
���EMC=60����
�ʴ�Ϊ30����60����
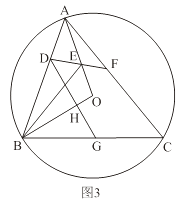
��2����CAF+��EMC=90�����������£�
����C��CH��GF�����CAF=��ACH��
��DE��GF��CH��GF��
��CH��DE��
���EMC=��HCM��
���EMC+��CAF=��MCH+��ACH=��ACB=90����

 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�