题目内容
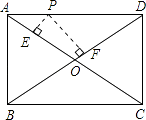
【题目】如图①,在矩形![]() 中,AB=30cm,BC=60cm.点
中,AB=30cm,BC=60cm.点![]() 从点
从点![]() 出发,沿
出发,沿![]() 路线向点
路线向点![]() 匀速运动,到达点
匀速运动,到达点![]() 后停止;点
后停止;点![]() 从点
从点![]() 出发,沿
出发,沿![]() 路线向点
路线向点![]() 匀速运动,到达点
匀速运动,到达点![]() 后停止.若点
后停止.若点![]() 同时出发,在运动过程中,
同时出发,在运动过程中,![]() 点停留了
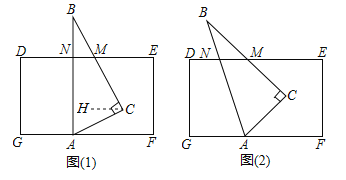
点停留了![]() ,图②是
,图②是![]() 两点在折线
两点在折线![]() 上相距的路程S(cm)与时间
上相距的路程S(cm)与时间![]() (s)之间的部分函数关系图象.求:
(s)之间的部分函数关系图象.求:
(1)P、Q两点的运动速度及P到C点的时间;
(2)设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的关系式.
之间的关系式.

【答案】(1) P点运动的速度为30![]() Q点运动的速度为15
Q点运动的速度为15![]() ;P到C点的时间为3s;(2)
;P到C点的时间为3s;(2)
【解析】
(1)利用函数图象得出当P、Q两点在函数关系图象上的F点到G点两点路程随时间变化减慢得出此时Q点停留,只有P点运动,再利用纵坐标的值得出P点和Q点运动速度;可求得P到C点的时间;
(2)根据P、Q的位置不同,进行分类讨论得出答案即可.
(1)由函数图象得出,当P、Q两点在F点到G点两点路程随时间变化减慢得出此时Q点停留1秒,只有P点运动,此时S的值由75下降到45,时间t=1s,
∴P点运动的速度为:![]() 30
30![]()
再根据函数图象E点到F点,S的值由120变为75,时间为t=1s,
∴![]() ,
,
∴Q点速度为:![]() ,
,
P到C点的时间:![]() ;
;
(2)当![]() 时,
时,
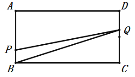
![]() ,
,
∴![]() ;
;
当![]() 时,P、B重合,
时,P、B重合,
∴![]() ;
;
当![]() 时,P点运动、Q点不动,
时,P点运动、Q点不动,

![]() ,
,![]() ,
,
∴![]() ;
;
当![]() 时,
时,
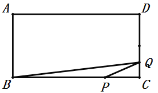
![]() ,
,![]() ,
,
∴![]() ;
;
当![]() 时,P、C、Q重合,
时,P、C、Q重合,
∴![]() ;
;
当![]() 时,
时,
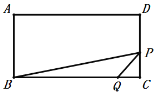
![]() ,
,![]() ,
,
∴![]() ;
;
当![]() 时,P到达终点D,
时,P到达终点D,
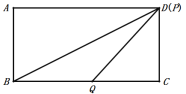
![]() ,
,
∴![]() ;
;
当![]() 时,B、Q重合,
时,B、Q重合,
∴![]() ;
;
当![]() 时,
时,

![]()
![]() ,
,
∴![]() ;
;
综上,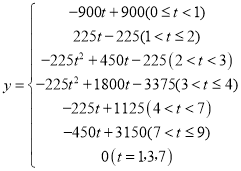 .
.

 阅读快车系列答案
阅读快车系列答案【题目】小颖和小红两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)试验,她们共做了60次试验,试验的结果如下:
朝上的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现的次数 | 7 | 9 | 6 | 8 | 20 | 10 |
(1)计算“3点朝上”的频率和“5点朝上”的频率.
(2)小颖说:“根据上述试验,一次试验中出现5点朝上的概率最大”;小红说:“如果投掷600次,那么出现6点朝上的次数正好是100次”.小颖和小红的说法正确吗?为什么?