题目内容
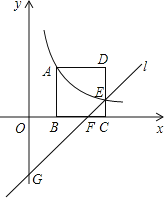
【题目】如图,正方形ABCD的顶点B,C在x轴的正半轴上,反比例函数y=![]() (k≠0)在第一象限的图象经过顶点A(m,2)和CD边上的点E(n,
(k≠0)在第一象限的图象经过顶点A(m,2)和CD边上的点E(n,![]() ),过点E的直线l交x轴于点F,交y轴于点G(0,﹣2),则点F的坐标是( )
),过点E的直线l交x轴于点F,交y轴于点G(0,﹣2),则点F的坐标是( )
A.(![]() ,0) B.(
,0) B.(![]() ,0) C.(
,0) C.(![]() ,0) D.(
,0) D.(![]() ,0)
,0)
【答案】C
【解析】
试题分析:由A(m,2)得到正方形的边长为2,则BC=2,所以n=2+m,根据反比例函数图象上点的坐标特征得到k=2m=![]() (2+m),解得m=1,则E点坐标为(3,
(2+m),解得m=1,则E点坐标为(3,![]() ),然后利用待定系数法确定直线GF的解析式为y=
),然后利用待定系数法确定直线GF的解析式为y=![]() x﹣2,再求y=0时对应自变量的值,从而得到点F的坐标.
x﹣2,再求y=0时对应自变量的值,从而得到点F的坐标.
解:∵正方形的顶点A(m,2),
∴正方形的边长为2,
∴BC=2,
而点E(n,![]() ),
),
∴n=2+m,即E点坐标为(2+m,![]() ),
),
∴k=2m=![]() (2+m),解得m=1,
(2+m),解得m=1,
∴E点坐标为(3,![]() ),
),
设直线GF的解析式为y=ax+b,
把E(3,![]() ),G(0,﹣2)代入得
),G(0,﹣2)代入得 ,解得
,解得 ,
,
∴直线GF的解析式为y=![]() x﹣2,
x﹣2,
当y=0时,![]() x﹣2=0,解得x=
x﹣2=0,解得x=![]() ,
,
∴点F的坐标为(![]() ,0).
,0).
故选:C.

练习册系列答案
相关题目