题目内容
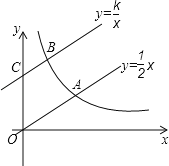
【题目】如图,直线![]() 与双曲线
与双曲线![]() (k>0,x>0)交于点A,将直线
(k>0,x>0)交于点A,将直线![]() 向上平移4个单位长度后,与y轴交于点C,与双曲线
向上平移4个单位长度后,与y轴交于点C,与双曲线![]() (k>0,x>0)交于点B.
(k>0,x>0)交于点B.
(1)设点B的横坐标分别为b,试用只含有字母b的代数式表示k;
(2)若OA=3BC,求k的值.
【答案】(1)k=![]() b2+4b;(2)k=
b2+4b;(2)k=![]() .
.
【解析】
试题分析:(1)根据平移的性质得出平移后直线的解析式为y=![]() x+4,由点B在直线y=
x+4,由点B在直线y=![]() x+4上,所以B(b,
x+4上,所以B(b,![]() b+4),点B在双曲线
b+4),点B在双曲线![]() (k>0,x>0)上,所以B(b,
(k>0,x>0)上,所以B(b,![]() ),从而得出
),从而得出![]() b+4=
b+4=![]() ,整理即可求得;
,整理即可求得;
(2)分别过点A、B作AD⊥x轴,BE⊥x轴,CF⊥BE于点F,再设设A(3x,![]() x),由于OA=3BC,故可得出B(x,
x),由于OA=3BC,故可得出B(x,![]() x+4),再根据反比例函数中k=xy为定值求出k的值即可.
x+4),再根据反比例函数中k=xy为定值求出k的值即可.
解:(1)∵将直线![]() 向上平移4个单位长度后,与y轴交于点C,
向上平移4个单位长度后,与y轴交于点C,
∴平移后直线的解析式为y=![]() x+4,
x+4,
∵点B在直线y=![]() x+4上,
x+4上,
∴B(b,![]() b+4),
b+4),
∵点B在双曲线![]() (k>0,x>0)上,
(k>0,x>0)上,
∴B(b,![]() ),
),
∴![]() b+4=
b+4=![]() ,
,
∴k=![]() b2+4b;
b2+4b;
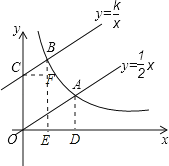
(2)分别过点A、B作AD⊥x轴,BE⊥x轴,CF⊥BE于点F,设A(3x,![]() x),
x),
∵OA=3BC,BC∥OA,CF∥x轴,
∴△BCF∽△AOD,
∴CF=![]() OD,
OD,
∵点B在直线y=![]() x+4上,
x+4上,
∴B(x,![]() x+4),
x+4),
∵点A、B在双曲线![]() 上,
上,
∴3x![]() x=x(
x=x(![]() x+4),解得x=1,
x+4),解得x=1,
∴k=3×1×![]() ×1=
×1=![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目