题目内容
【题目】已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(1,0),B点坐标为(5,0)点C(0,5),M为它的顶点.
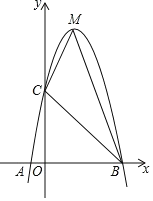
(1)求抛物线的解析式;
(2)求△MCB的面积.
【答案】(1)y= -x2+4x+5;(2)15
【解析】
(1)设交点式y=a(x+1)(x-5),然后把C(0,5)代入求出a即可得到抛物线解析式;
(2)先把解析式配成顶点式,然后写出M点的坐标,再过M作MD⊥x轴,根据△MCB的面积=梯形MCOD的面积+△MDB的面积-△COB的面积求解.
(1)设y=a(x+1)(x-5),代入(0,5),得:a= -1
y= -(x+1)(x-5),
∴y= -x2+4x+5
(2)y=-x2+4x+5=-(x-2)2+9,则M(2,9),
所以顶点M(2,9);
过M作MD⊥x轴,如图,

∵A点坐标为(1,0),B点坐标为(5,0)
∴AB=6,AD=BD=3
∴OD=2
又C(0,5),
∴△MCB的面积=梯形MCOD的面积+△MDB的面积-△COB的面积
=![]()
=14+13.5-12.5
=15.

练习册系列答案
相关题目