题目内容
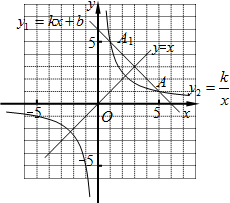 如图,在方格纸中建立直角坐标系,已知一次函数y1=-x+b的图象与反比例函数y2=
如图,在方格纸中建立直角坐标系,已知一次函数y1=-x+b的图象与反比例函数y2=| k |
| x |
(1)求这两个函数的关系式;
(2)由反比例函数y2=
| k |
| x |
分析:(1)将点A(5,1)分别代入一次函数y1=-x+b与反比例函数y2=
中,可求b、k的值,确定两个函数解析式;
(2)抛物线关于直线y=x轴对称,可证直线y1=-x+6与直线y=x互相垂直,根据轴对称性可求点A1的坐标,再根据y1与y2的图象的位置关系,求x的取值范围.
| k |
| x |
(2)抛物线关于直线y=x轴对称,可证直线y1=-x+6与直线y=x互相垂直,根据轴对称性可求点A1的坐标,再根据y1与y2的图象的位置关系,求x的取值范围.
解答:解:(1)∵点A(5,1)是一次函数y1=-x+b图象与反比例函数y2=
图象的交点,
∴-5+b=1,
=1,
解得b=6,k=5,
∴y1=-x+6,y2=
;
(2)由函数图象可知A1(1,5),
当0<x<1或x>5时,y1<y2.
| k |
| x |
∴-5+b=1,
| k |
| 5 |
解得b=6,k=5,
∴y1=-x+6,y2=
| 5 |
| x |
(2)由函数图象可知A1(1,5),
当0<x<1或x>5时,y1<y2.
点评:本题考查了反比例函数与一次函数的交点问题.关键是利用待定系数法求两个函数解析式,结合图象的位置,对称性求解.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
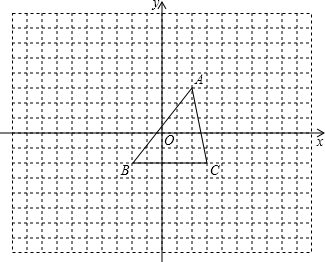 如图,在方格纸中建立平面直角坐标系后,点B的坐标为(-2,-2).
如图,在方格纸中建立平面直角坐标系后,点B的坐标为(-2,-2).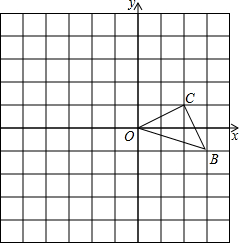 如图,在方格纸中建立直角坐标系,△BOC的O点与坐标原点重合,其余两点落在格点上且每个方格是边长为单位1的正方形
如图,在方格纸中建立直角坐标系,△BOC的O点与坐标原点重合,其余两点落在格点上且每个方格是边长为单位1的正方形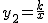 的图象相交于点A(5,1)和A1.
的图象相交于点A(5,1)和A1.