题目内容
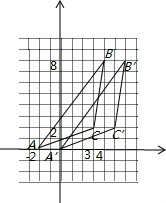
18、如图,在方格纸中建立平面直角坐标系,已知△ABC三点坐标分别是:点A(-2,0),点B(4,8),点C(3,2).
(1)在方格纸中画出△ABC.
(2)将△ABC向右平移两个单位,作出平移后的△A′B′C′.
(3)写出两条反映△ABC与△A′B′C′之间关系的性质,例如:“△ABC与△A′B′C′的对应角相等.”
①
②

(1)在方格纸中画出△ABC.
(2)将△ABC向右平移两个单位,作出平移后的△A′B′C′.
(3)写出两条反映△ABC与△A′B′C′之间关系的性质,例如:“△ABC与△A′B′C′的对应角相等.”
①
△ABC与△A′B′C′对应边相等
②
AA′与BB′平行且相等
.分析:(1)结合坐标系找出A,B,C三点坐标连接即可;
(2)利用平移的性质平移A,B,C三点即可得出答案;
(3)利用平移的性质得出答案即可.
(2)利用平移的性质平移A,B,C三点即可得出答案;
(3)利用平移的性质得出答案即可.
解答:解:(1)如图所示;

(2)如图所示;
(3)答案不唯一
①△ABC与△A′B′C′对应边相等;
②AA′与BB′平行且相等.

(2)如图所示;

(3)答案不唯一
①△ABC与△A′B′C′对应边相等;
②AA′与BB′平行且相等.
点评:此题主要考查了图象的平移以及点的坐标确定方法,根据平移性质正确平移三角形是解决问题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
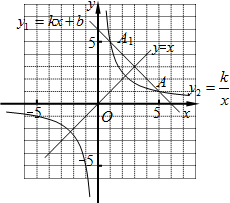 如图,在方格纸中建立直角坐标系,已知一次函数y1=-x+b的图象与反比例函数
如图,在方格纸中建立直角坐标系,已知一次函数y1=-x+b的图象与反比例函数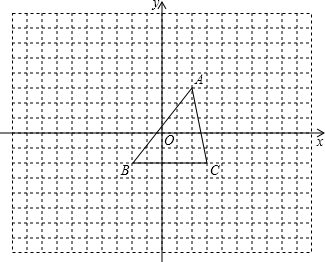 如图,在方格纸中建立平面直角坐标系后,点B的坐标为(-2,-2).
如图,在方格纸中建立平面直角坐标系后,点B的坐标为(-2,-2).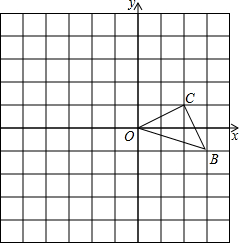 如图,在方格纸中建立直角坐标系,△BOC的O点与坐标原点重合,其余两点落在格点上且每个方格是边长为单位1的正方形
如图,在方格纸中建立直角坐标系,△BOC的O点与坐标原点重合,其余两点落在格点上且每个方格是边长为单位1的正方形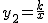 的图象相交于点A(5,1)和A1.
的图象相交于点A(5,1)和A1.