Question

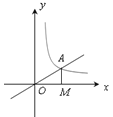
【题目】如图所示，正比例函数y=x的图象与反比例函数y=（k≠0）在第一象限的图象交于点，过点A作X轴的垂线，垂足为M，已知△AOM的面积为1．

（1）求反比例函数的解析式；

（2）如果点为反比例函数在第一象限图象上的点（点与点不重合），且点的横坐标为1，在轴上求一点，使最小．

Answer 1

【答案】（1）y=；（2）P点坐标为（，0）

【解析】

试题分析：（1） 设A点的坐标为（a，b），于是ab=k ．又由△AOM的面积为1．得到ab=1 ，∴k=1 ．进而求得k值，确定反比例函数解析式；（2）由两个函数解析式求得交点A的坐标，又由B点的横坐标为1，及反比例函数解析式求得B点坐标，作A点关于x轴的对称点C，连接BC，交x轴于一点，即为符合要求的P点，然后由B，C两点坐标求出直线BC的解析式，即可求出P点坐标．

试题解析：（1）根据题意可设A点的坐标为（a，b），则b=．∴ab=k ．

∵△AOM的面积为1．

∴ab=1 ，

∴k=1 ．

∴ k=2．

∴ 反比例函数的解析式为y=；

（2） 由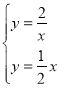 得或，

∵A在第一象限，

∴ A为（2，1），设A点关于x轴的对称点为C，

则C点的坐标为（2，-1）如要在x轴上求一点P，使PA+PB最小．

则P点应为BC和x轴的交点，

如图所示．设直线BC的解析式为y=mx+n．

∵ B为（1，2），

∴，解得：，

∴ BC的解析式为y=-3x+5．

当y=0时，x=．

∴ P点坐标为（，0）