��Ŀ����
�¶��壺��x0=ax02+bx0+c��������Ƶ㣨x0��x0��Ϊ������y=ax2+bx+c ��a��0���ϵIJ����㣮��������C�Ľ���ʽΪ��y=ax2+��b+1��x+��b-1������a��0��
��1��������C���㣨0��-3���������������C����ƽ�� ����λ���䶥��ǡ����y���ϣ���������C�Ľ���ʽ�����ϵIJ����㣻
����λ���䶥��ǡ����y���ϣ���������C�Ľ���ʽ�����ϵIJ����㣻
��2����������ʵ��b��ʵ��aӦ��ʲô��Χ�ڣ�����ʹ������C������������ͬ�IJ����㣿
��3����aΪ������������a+b+1=0����������C��x��������ĺ�����ֱ�Ϊx1��x2���Ƿ��������k��ʹ�� 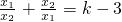 �����������ڣ����k��ֵ���������ڣ���˵�����ɣ�
�����������ڣ����k��ֵ���������ڣ���˵�����ɣ�
�⣺��1��������ó���
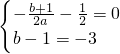 ��
��
��ã� ��
��
�������߽���ʽΪ��y=x2-x-3��
��x=x2-x-3��
��ã�x1=-1��x2=3��
�����Ϊ����-1��-1���ͣ�3��3����
��2����������C��������ͬ�Ķ��㣬
��x=ax2+��b+1��x+��b-1����
�����ã�ax2+bx+��b-1��=0��
��������C��������ͬ�㣬
�����0��
��b2-4a��b-1����0��
b2-4ab+4a��0��
��bΪ����ʵ������ʹ����ʽ������
�����-4a��2-4��1��4a��0��
�����ã�a2-a��0��
�Ӷ����� ��
��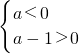 ��
��
��ã�0��a��1��
��ʵ��a��ȡֵ��ΧӦΪ��0��a��1��
��3����a+b+1=0����b=-a-1����������C����y=ax2-ax-��a+2����
��x1��x2��������C��x��Ľ�������꣬
���=a2+4a��a+2����0��
��ã�a��0��a��- ��
��
�ɸ���ϵ���Ĺ�ϵ�ã�
x1+x2=1��x1•x2=- ��
��
��k=3+ +
+ =3+
=3+ =
= ��a��0��a��-
��a��0��a��- ����a������
����a������
ҪʹkΪ������ȡa=-4��-3��-1��0������a=-1��0����������ȥ��
�����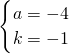 ��
��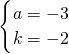 ��
��
��������1��������֪�ó�b-1=-3��- =
= �����ɵó�a��b��ֵ�������ó�ͼ���ϵIJ����㣻
�����ɵó�a��b��ֵ�������ó�ͼ���ϵIJ����㣻
��2������������C��������ͬ�Ķ��㣬�ó�x=ax2+��b+1��x+��b-1����������������C��������ͬ�㣬�ó�����0����b2-4a��b-1����0��
��bΪ����ʵ������ʹ����ʽ����������У�-4a��2-4��1��4a��0�������ó�a��ȡֵ��Χ��
��3�����ȸ���x1��x2��������C��x��Ľ�������꣬�ó���=a2+4a��a+2����0�������ø�����ϵ����ϵ�����a��ȡֵ���ɣ�
������������Ҫ�����˶��κ������ۺ�Ӧ���Լ�����ϵ���Ĺ�ϵ�Ͳ���ʽ��Ľⷨ�������б�ʽ�ɼ������֪ʶ����ȷ�ó�����ʽ�⼯�ǽ���ؼ���
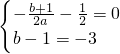 ��
����ã�
 ��
���������߽���ʽΪ��y=x2-x-3��
��x=x2-x-3��
��ã�x1=-1��x2=3��
�����Ϊ����-1��-1���ͣ�3��3����
��2����������C��������ͬ�Ķ��㣬
��x=ax2+��b+1��x+��b-1����
�����ã�ax2+bx+��b-1��=0��
��������C��������ͬ�㣬
�����0��
��b2-4a��b-1����0��
b2-4ab+4a��0��
��bΪ����ʵ������ʹ����ʽ������
�����-4a��2-4��1��4a��0��
�����ã�a2-a��0��
�Ӷ�����
 ��
��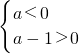 ��
����ã�0��a��1��
��ʵ��a��ȡֵ��ΧӦΪ��0��a��1��
��3����a+b+1=0����b=-a-1����������C����y=ax2-ax-��a+2����
��x1��x2��������C��x��Ľ�������꣬
���=a2+4a��a+2����0��
��ã�a��0��a��-
 ��
���ɸ���ϵ���Ĺ�ϵ�ã�
x1+x2=1��x1•x2=-
 ��
����k=3+
 +
+ =3+
=3+ =
= ��a��0��a��-
��a��0��a��- ����a������
����aΪ������ҪʹkΪ������ȡa=-4��-3��-1��0������a=-1��0����������ȥ��
�����
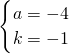 ��
��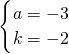 ��
����������1��������֪�ó�b-1=-3��-
 =
= �����ɵó�a��b��ֵ�������ó�ͼ���ϵIJ����㣻
�����ɵó�a��b��ֵ�������ó�ͼ���ϵIJ����㣻��2������������C��������ͬ�Ķ��㣬�ó�x=ax2+��b+1��x+��b-1����������������C��������ͬ�㣬�ó�����0����b2-4a��b-1����0��
��bΪ����ʵ������ʹ����ʽ����������У�-4a��2-4��1��4a��0�������ó�a��ȡֵ��Χ��
��3�����ȸ���x1��x2��������C��x��Ľ�������꣬�ó���=a2+4a��a+2����0�������ø�����ϵ����ϵ�����a��ȡֵ���ɣ�
������������Ҫ�����˶��κ������ۺ�Ӧ���Լ�����ϵ���Ĺ�ϵ�Ͳ���ʽ��Ľⷨ�������б�ʽ�ɼ������֪ʶ����ȷ�ó�����ʽ�⼯�ǽ���ؼ���

��ϰ��ϵ�д�
�����Ŀ
 ����λ���䶥��ǡ����y���ϣ���������C�Ľ���ʽ�����ϵIJ����㣻
����λ���䶥��ǡ����y���ϣ���������C�Ľ���ʽ�����ϵIJ����㣻 �����������ڣ����k��ֵ���������ڣ���˵������.
�����������ڣ����k��ֵ���������ڣ���˵������.  ����λ���䶥��ǡ����y���ϣ���������C�Ľ���ʽ�����ϵIJ����㣻
����λ���䶥��ǡ����y���ϣ���������C�Ľ���ʽ�����ϵIJ����㣻 �����������ڣ����k��ֵ���������ڣ���˵������.
�����������ڣ����k��ֵ���������ڣ���˵������.