题目内容
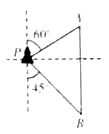
【题目】如图,一艘海轮位于灯塔![]() 的北偏东
的北偏东![]() 方向,距离灯塔
方向,距离灯塔![]() 的
的![]() 处,它沿正南方向航行一段时间后,到达位于灯塔
处,它沿正南方向航行一段时间后,到达位于灯塔![]() 的南偏东
的南偏东![]() 方向上的
方向上的![]() 处.此时,
处.此时,![]() 处与灯塔
处与灯塔![]() 的距离约为
的距离约为 ![]() .(结果取整数,参考数据:
.(结果取整数,参考数据:![]() )
)
【答案】102.
【解析】
试题分析:根据题意得出∠MPA=∠PAD=60°,从而知PD=APsin∠PAD=43![]() ,由∠BPD=∠PBD=45°根据BP=
,由∠BPD=∠PBD=45°根据BP=![]() ,即可求出即可.
,即可求出即可.
过P作PD⊥AB,垂足为D,
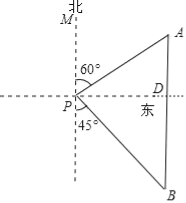
∵一艘海轮位于灯塔P的北偏东60°方向,距离灯塔86n mile的A处,
∴∠MPA=∠PAD=60°,∴PD=APsin∠PAD=86×![]() =43
=43![]() ,
,
∵∠BPD=45°,∴∠B=45°.
在Rt△BDP中,由勾股定理,得BP=![]() =
=![]() =43
=43![]() ×
×![]() ≈102(n mile).
≈102(n mile).
故答案为102.

练习册系列答案
相关题目