题目内容
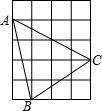如图，正方形网格中，每个小正方形的边长为1，在网格上的三角形ABC中，点B到AC的距离是分析：先根据图形，用求差法求出△ABC的面积．再用勾股定理求出AC，然后根据面积公式解答即可．
解答：解：由图可知：三角形ABC的面积=大矩形的面积-上面的梯形的面积-两边的两个小直角三角形的面积，由此可以得出
S△ABC=4×5-（1+3）×4÷2-1×4÷2-2×3÷2=7
又因为三角形ABC的面积=AC×AC边上的高（B到AC的距离）÷2
根据勾股定理AC=
=2
BC到AC的距离=S△ABC÷AC×2=7÷2
×2=
．
S△ABC=4×5-（1+3）×4÷2-1×4÷2-2×3÷2=7
又因为三角形ABC的面积=AC×AC边上的高（B到AC的距离）÷2
根据勾股定理AC=
| 22+42 |
| 5 |
BC到AC的距离=S△ABC÷AC×2=7÷2
| 5 |
7
| ||
| 5 |
点评：本题主要考查了勾股定理的运用，本题中得出三角形ABC的面积是解题的关键．
练习册系列答案
相关题目
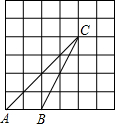在如图的正方形网格中有一个格点三角形ABC．请在图中画一个与△ABC相似且相似比不等于1的格点三角形，并写出它们的相似比．
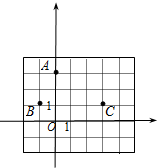22、如图，正方形网格中，A、B、C均在格点上，在所给直角坐标系中解答下列问题：
如图，正方形网格中，每一个小正方形的边长都是1，四边形ABCD的四个顶点都在格点上，O为AD边的中点，若把四边形ABCD绕着点O顺时针旋转180°．试解决下列问题：
在如图的正方形网格中，每个小正方形的边长都是单位1，△ABC的顶点均在格点上．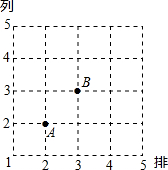
如图，正方形网格中的交点，我们称之为格点，点A用有序数对（2，2）表示，其中第一个数表示排数，第2个数表示列数，在图中有一个格点C，使S△ABC=1，写出符合条件的点C的有序数对．