题目内容
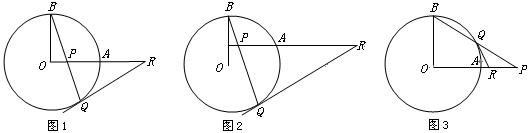
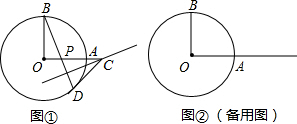
如图①,OA和OB是⊙O的半径,且OA⊥OB,P是OA上的任意一点,BP的延长线交⊙O于D,PD的垂直平分线交OA的延长线于点C,连接CD.
(1)求证:CD是⊙O的切线;
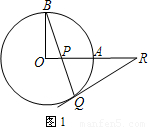
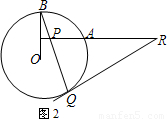
(2)若P是OA延长线上的任意一点,其他条件不变,CD还是⊙O的切线吗?如果是,在备用图②中作出相应图形(请保留作图痕迹),并论证.
(1)求证:CD是⊙O的切线;
(2)若P是OA延长线上的任意一点,其他条件不变,CD还是⊙O的切线吗?如果是,在备用图②中作出相应图形(请保留作图痕迹),并论证.

分析:(1)连接DO,首先利用垂直平分线的性质得出∠CDP=∠BPO,进而利用切线的判定求出即可;
(2)根据已知得出图象进而求出∠2+∠3=90°,即可得出答案.
(2)根据已知得出图象进而求出∠2+∠3=90°,即可得出答案.
解答: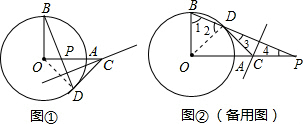 (1)证明:连OD.
(1)证明:连OD.
∵PC=CD,
∴∠CPD=∠CDP而∠CPD=∠BPO,
∴∠CDP=∠BPO,
又∵OB=OD,
∴∠ODB=∠OBD,
∵∠OBP+∠OP B=90°,
∴∠ODC=∠ODP+∠CDP=90°,
∴CD是⊙O的切线;
(2)如图所示:
证明:连OD.
∵CD=CP,
∴∠3=∠4,
同理:∠1=∠2,
而∠1+∠4=90°从而得∠2+∠3=90°,
∴∠ODC=90°,
∴CD是⊙O的切线.
 (1)证明:连OD.
(1)证明:连OD.∵PC=CD,
∴∠CPD=∠CDP而∠CPD=∠BPO,
∴∠CDP=∠BPO,
又∵OB=OD,
∴∠ODB=∠OBD,
∵∠OBP+∠OP B=90°,
∴∠ODC=∠ODP+∠CDP=90°,
∴CD是⊙O的切线;
(2)如图所示:
证明:连OD.
∵CD=CP,
∴∠3=∠4,
同理:∠1=∠2,
而∠1+∠4=90°从而得∠2+∠3=90°,
∴∠ODC=90°,
∴CD是⊙O的切线.
点评:此题主要考查了切线的判定与垂直平分线的性质,熟练利用切线的判定定理求出是解题关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目