题目内容
如图,在□ABCD中,AB=4,AD=6,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG= .
.

(1)求AE的长; (2)求ΔCEF的周长和面积.
 .
.
(1)求AE的长; (2)求ΔCEF的周长和面积.
(1)AE=4;(2)△CEF的周长=6,△CEF的面积=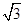 .
.
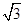 .
.试题分析:(1)由于AE平分∠BAD,那么∠BAE=∠DAE,由AD∥BC,可得内错角∠DAE=∠BEA,等量代换后可证得AB=BE,即△ABE是等腰三角形,根据等腰三角形“三线合一”的性质得出AE=2AG,而在Rt△ABG中,由勾股定理可求得AG的值,即可求得AE的长;
(2)首先证明△ABE∽△FCE,再分别求出△ABE的周长和面积,然后根据相似比等于周长比,面积比等于相似比的平方即可得到答案.
试题解析:(1)∵AE平分∠BAD,
∴∠DAE=∠BAE;
又∵AD∥BC,
∴∠BEA=∠DAE=∠BAE,
∴AB=BE=4,
∵BG⊥AE,垂足为G,
∴AE=2AG.
在Rt△ABG中,∵∠AGB=90°,AB=4,BG=2
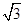 ,
,∴AG==2,
∴AE=2AG=4;
(2)∵BE=4,BC=AD=6,
∴CE=BC﹣BE=6﹣4=2,
∴BE:CE=4:2=2:1.
∵AB∥FC,
∴△ABE∽△FCE,
∴△ABE的周长:△CEF的周长=BE:CE=2:1,
△ABE的面积:△CEF的面积=(BE:CE)2=4:1,
∵AB=BE=4,AE=4,BG=2
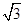 ,
,∴△ABE的周长=4+4+4=12,△ABE的面积=
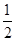 ×4×2
×4×2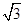 =4
=4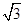 ,
,∴△CEF的周长=6,△CEF的面积=
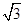 .
.
练习册系列答案
相关题目
 =
= =
= =k,则k的值是
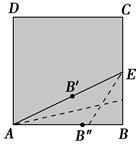
=k,则k的值是 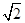 .一动点P从点B出发,沿BC方向以每秒1个单位长度的速度匀速运动,到达点C即停止.在整个运动过程中,过点P作PD⊥BC与Rt△ABC的直角边相交于点D,延长PD至点Q,使得PD=QD,以PQ为斜边在PQ左侧作等腰直角三角形PQE.设运动时间为t秒(t>0).
.一动点P从点B出发,沿BC方向以每秒1个单位长度的速度匀速运动,到达点C即停止.在整个运动过程中,过点P作PD⊥BC与Rt△ABC的直角边相交于点D,延长PD至点Q,使得PD=QD,以PQ为斜边在PQ左侧作等腰直角三角形PQE.设运动时间为t秒(t>0).
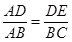 ,请添加一个条件,使
,请添加一个条件,使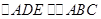 ,这个条件可以是______.
,这个条件可以是______.

 ,它的实际长度约为( )
,它的实际长度约为( ) ;
;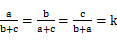 ,则直线
,则直线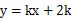 一定经过( )
一定经过( )