题目内容
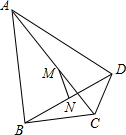如图在四边形ABCD中，∠ABC=∠ADC=90°，M、N分别是AC、BD的中点，猜一猜MN与BD的位置关系，再证明你的结论．
MN与BD的位置关系是MN垂直且平分BD，
证明：连接BM、DM，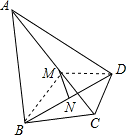
∵∠ABC=90°，∠ADC=90°，M为AC中点，
∴BM=
AC，DM=AC，
∴BM=DM，
∵N为BD中点，
∴MN⊥BD，BN=DN，
即MN与BD的位置关系是MN垂直且平分BD．
分析：连接BM、DM，根据直角三角形斜边上中线性质推出BM=AC，DM=AC，推出BM=DM，在△BMD中，根据三线合一定理求出即可．
点评：本题考查了等腰三角形性质和直角三角形斜边上中线的应用，关键是求出BM=DM，题目比较典型，主要考查学生运用性质进行推理的能力．
证明：连接BM、DM，
∵∠ABC=90°，∠ADC=90°，M为AC中点，
∴BM=
AC，DM=AC，∴BM=DM，
∵N为BD中点，
∴MN⊥BD，BN=DN，
即MN与BD的位置关系是MN垂直且平分BD．
分析：连接BM、DM，根据直角三角形斜边上中线性质推出BM=
AC，DM=AC，推出BM=DM，在△BMD中，根据三线合一定理求出即可．点评：本题考查了等腰三角形性质和直角三角形斜边上中线的应用，关键是求出BM=DM，题目比较典型，主要考查学生运用性质进行推理的能力．
练习册系列答案
相关题目
22、已知：如图在四边形ABCD中，∠A=∠D、∠B=∠C，试判断AD与BC的位置关系，并说明理由．
如图在四边形ABCD中，E是对角线BD上一点，EF∥AD，EM∥BC，则
如图在四边形ABCD中，∠ACB+∠ADB=180°，∠ABC=∠BAC=60°．
如图在四边形ABCD中，∠1和∠2分别是∠A和∠C的外角，且∠B+∠D=140°，则∠1+∠2=
度数？如果能请求出∠A的度数，如果不能请补充一个条件使其能求出∠A的度数，请完善解题过程