题目内容
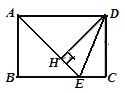
【题目】如图，在矩形ABCD中，AD=
AB，∠BAD的平分线交BC于点E，DH⊥AE于点H，连接DE，下列结论：①∠AED=∠CED；②
AED为等腰三角形；③EH=CE；④图中有3个等腰三角形.结论正确的个数为（ ）
A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】试题分析：设AB=1，则根据角平分线的性质可得：BE=AE=1，则AE=
，根据题意可得：AD=
，则△AED为等腰三角形；则∠AED=∠ADE，根据平行线的性质可得：∠ADE=∠DEC，则∠AED=∠CED；根据∠AED=∠CED，∠DHE=∠C=90°，DE=DE可得：△HDE和△CDE，则EH=CE；根据题意可得：△ABE、△AHD和△ADE为等腰三角形，则题中的4个都正确.
练习册系列答案
名校课堂系列答案
相关题目
【题目】已知二次函数y=ax2+bx+c中，函数y与自变量x的部分对应值如下表：
x | … | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | 10 | 5 | 2 | 1 | 2 | 5 | … |
若A（m，y1），B（m﹣2，y2）两点都在该函数的图象上，当m=时，y1=y2 ．