题目内容
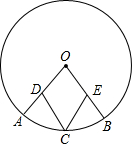 如图,D、E分别为⊙O半径OA、OB的中点,C是
如图,D、E分别为⊙O半径OA、OB的中点,C是 的中点,CD与CE相等吗?为什么?
的中点,CD与CE相等吗?为什么?
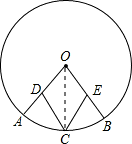 解:CD=CE,理由如下:(1分)
解:CD=CE,理由如下:(1分)连接OC,
∵D、E分别为⊙O半径OA、OB的中点,
∴OD=
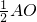 ,
,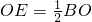 ,
,∵OA=OB,∴OD=OE,(2分)
∵C是
 的中点,∴
的中点,∴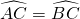 ,
,∴∠AOC=∠BOC,(4分)
∴△DCO≌△ECO,(5分)
∴CD=CE.(6分)
故答案为:CD=CE.
分析:连接OC,由已知条件可得出OD=OE,
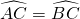 ,再由同弧所对的圆周角相等可得到∠AOC=∠BOC,由全等三角形的判定定理可得出△DCO≌△ECO,再根据全等三角形的对应边相等即可求出答案.
,再由同弧所对的圆周角相等可得到∠AOC=∠BOC,由全等三角形的判定定理可得出△DCO≌△ECO,再根据全等三角形的对应边相等即可求出答案.点评:本题考查的是圆心角、弧、弦的关系,解答此题的关键是连接OC,构造出圆心角,再由同弧或等弧所对的圆心角相等即可解答.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
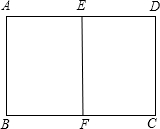 如图,E,F分别为矩形ABCD的边AD,BC的中点,若矩形ABCD∽矩形EABF,AB=1.求矩形ABCD
如图,E,F分别为矩形ABCD的边AD,BC的中点,若矩形ABCD∽矩形EABF,AB=1.求矩形ABCD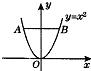 5、如图,A、B分别为y=x2上两点,且线段AB⊥y轴,若AB=6,则直线AB的表达式为( )
5、如图,A、B分别为y=x2上两点,且线段AB⊥y轴,若AB=6,则直线AB的表达式为( )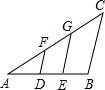 如图,D,E分别为AB的三等分点,DF∥EG∥BC,若BC=12,则DF=
如图,D,E分别为AB的三等分点,DF∥EG∥BC,若BC=12,则DF= 如图,D、E分别为⊙O半径OA、OB的中点,C是
如图,D、E分别为⊙O半径OA、OB的中点,C是
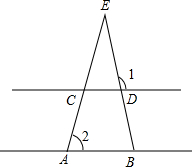 (2012•朝阳)如图,C、D分别为EA、EB的中点,∠E=30°,∠1=110°,则∠2的度数为( )
(2012•朝阳)如图,C、D分别为EA、EB的中点,∠E=30°,∠1=110°,则∠2的度数为( )